Month: July 2020

27
Jul
2020
Utilização do Modelo GARCH(1,1) na Previsão de Volatilidade

Utilização do Modelo GARCH(1,1) na Previsão de Volatilidade

O objetivo deste artigo é trazer um entendimento sobre o que se trata o modelo GARCH e apresentar uma aplicação em python deste modelo para a previsão de volatilidade. Vamos começar compreendendo como o modelo surgiu e como se destaca em comparação às outras formas de estimar a volatilidade. Em seguida, vamos explicar as propriedades do modelo GARCH(1,1) que será utilizado em nossa aplicação. Por fim, iremos demonstrar como montar a aplicação do modelo em python.

 

A motivação para este artigo foi a relevância que a volatilidade possui atualmente para os estudos de previsão de riscos. Um dos momentos de reconhecimento da importância de se mensurar o efeito da volatilidade ao longo do tempo na análise de riscos, ocorreu quando Robert Engle recebeu o Prêmio Nobel de Economia em 2003, por desenvolver um método estatístico para lidar com esta propriedade das séries econômicas. A Academia Real Sueca de Ciências afirmou que:

 

“Os modelos ARCH de Engle se tornaram ferramentas indispensáveis não apenas para pesquisas, mas também para analistas do mercado financeiro, que os utilizam na formação de ativos e na avaliação de risco de portfólio”.

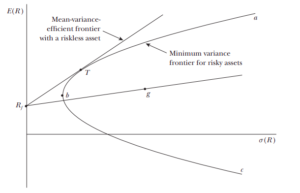
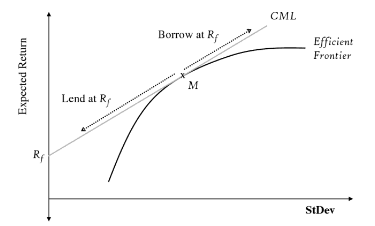
Por que utilizar o Modelo GARCH para modelagem da volatilidade?

Uma mudança na variância ou volatilidade ao longo do tempo pode causar problemas na modelagem de séries temporais com métodos clássicos. Pois, um aspecto de uma série temporal que esses modelos não captam é uma alteração na variância ao longo do tempo, devido ao fato de que nesses modelos as observações recentes receberiam o mesmo peso que observações mais antigas, que claramente podem não possuir o mesmo impacto ao longo do tempo que uma vez tiveram.

 

É por isso que métodos de estimativa de volatilidade evoluíram para modelos que dão mais peso às informações recentes. Desses primeiros modelos se destacam a família de modelos GARCH, inicialmente proposto por Engle (1982), como ARCH, e generalizado por Bollerslev (1986). Esses métodos fornecem uma maneira de modelar uma mudança na variância de uma série temporal dependente do tempo.


A principal diferença entre eles seria o fato de que enquanto o modelo ARCH(q) demonstra que a variância condicional, ou volatilidade, σt2, em um determinado período, depende da magnitude de uma série de retornos ao quadrado (ou erros quadráticos), rt2, em “q” períodos anteriores, o modelo GARCH(p,q) vai além com componente adicional, sendo este a variância condicional em “p” períodos anteriores. A seguir a equação da variância condicional definida pelo modelo ARCH(q):

1

O modelo GARCH (p,q) possui um termo autorregressivo, como em ARCH(q), com a adição de um termo de média móvel. O termo autorregressivo (p) modela a variância condicional dos erros quadráticos ou simplesmente modela a variância condicional da série temporal ao quadrado, já a parte de média móvel (q) modela a variação do processo. A seguir a equação da variância condicional definida pelo modelo GARCH(p,q):

2

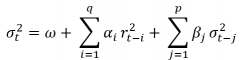
Outro motivo relevante para se usar o modelo GARCH, é que ele pode capturar a aglomeração da volatilidade, ou clusters de volatilidade, sofrida por séries financeiras. Os preços dos ativos são caracterizados por esse fenômeno, que se trata de períodos nos quais os preços exibem grandes variações para um longo período seguido por um período de tranquilidade comparativa.

 

Existem hoje muitas variantes do modelo GARCH, a maioria das quais fornece apenas melhorias marginais no modelo original. Entre essas extensões do modelo GARCH, estão o Integrated GARCH, Exponential GARCH ou EGARCH, GJR-GARCH e outras. A família de modelos GARCH é amplamente utilizada na prática para prever a volatilidade e os retornos do mercado financeiro.



O modelo

Para a maioria das séries financeiras, a utilização do modelo GARCH(1,1) já é suficiente para explicar sua volatilidade, desta forma, para a aplicação que será demonstrada mais a frente, utilizaremos este modelo. Para explicar o modelo, inicialmente consideramos rt como uma série de retornos, partindo disso o modelo GARCH(1.1) é definido como:

3

A equação acima demonstra que o modelo contém um termo defasado de retorno ao quadrado, rt-12, como em ARCH(1), mas também um termo defasado da variação condicional, σt-12, para determinar a variação condicional no período t, σt2.


O termo alfa, α, indica quanto o último retorno observado tem de influência sobre a variância condicional hoje, já o termo beta, β, indica quanto a volatilidade do período anterior deve influenciar a volatilidade hoje. Quanto maior o alfa maior o impacto imediato de choques nos dados da série temporal e quanto maior o beta maior a duração do impacto. Para a estimação dos parâmetros, é utilizado o método de máxima verossimilhança.

 

Uma propriedade este modelo é que todos os parâmetros não são negativos, ω, α, β ≥ 0. Para que o modelo seja estacionário, a soma dos parâmetros alfa e beta deve ser menor que um,  α + β < 1.

Ômega, ω, pode ser a visto como seria a variação se as informações sobre variações passadas não estivessem sendo passadas para o modelo. Ômega também é definido como o produto de um termo gama, γ, e da variância incondicional ou variância de longo prazo, σLR. Enquanto ômega, alfa e beta são os parâmetros de volatilidade do modelo, gama pode ser chamado de parâmetro de assimetria do modelo.

4

A equação acima nos mostra que, para existir a variância incondicional de rt2, é necessário que α + β < 1, justificando a restrição de estacionariedade do modelo. É utilizada a expressão a seguir para se estimar um valor para a variância condicional em um período t+i, em outras palavras, está é a fórmula para prever a volatilidade dos próximos períodos.

5

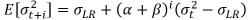
Utilizaremos o log-retorno devido a suas propriedades estatísticas, como a estacionariedade, para calcular os retornos da série temporal.

6

A aplicação em Python

A estimação dos parâmetros e o cálculo para prever a volatilidade serão feitos a seguir, utilizaremos o ambiente do Google Colab e a cotação do dólar será o nosso objeto de estudo.

 

Inicialmente temos que instalar e importar os pacotes que iremos utilizar:

 

 

#Instalação e importação dos pacotes para os buscar os dados e as funções do modelo

!pip install quandl

!pip install arch

import quandl as qdl

from arch import arch_model

 

#Importação de bibliotecas matemáticas e de ciência de dados

import numpy as np

import pandas as pd

 

#Pré definição das configuração dos gráficos

import seaborn as sns

sns.set()

import matplotlib as mpl

mpl.rcParams[‘figure.figsize’] = (15, 5)

 

 

 

Utilizamos o pacote quandl para buscar os dados das cotações do dólar.

 

 

#Definição dos dados

dolar = qdl.get(‘BCB/1’, start_date = ‘2000-01-01’)

 

#Visualização do gráfico das cotações

dolar.rename(columns={“Value”: “USD”}, inplace=True)

dolar.plot()

 

 

 

 

#Visualização do gráfico dos retornos

dolar_ret = np.log(dolar/dolar.shift(1)).dropna()

dolar_ret.plot()

 

 


Para esta análise será necessário padronizar os retornos, subtraindo-os de sua média esperada e dividindo pelo seu desvio padrão.

 

 

#Padronização dos retornos

dolar_m = dolar_ret.values.mean()

dolar_dp = dolar_ret.values.std()

dolar_ret_p = (dolar_ret – dolar_m)/dolar_dp

 

 

 

Para estimar um modelo do tipo GARCH, selecionamos a função arch_model do pacote arch instalado anteriormente. A função arch_model pode especificar um modelo GARCH em vez do modelo ARCH se informamos o modelo de volatilidade a ser utilizado, especificando o seguinte argumento da função  vol = ‘GARCH’, assim como os argumentos de defasagem p=1 e q=1 para determinar um modelo GARCH(1,1):

 

 

#Aplicação do Modelo GARCH(1,1) aos dados e vizualização dos resultados

garch_model = arch_model(dolar_ret_p, p=1, q=1, vol=‘GARCH’, dist=‘Normal’)

resultados = garch_model.fit(disp=‘off’)

print(resultados.summary())

 


 

 

#Previsão da volatilidade

resultados_forecast = resultados.forecast(horizon=5)

print(resultados_forecast.variance[-1:])


Cada coluna “h.n” da saída da previsão corresponde a n d períodos a frente, neste caso n dias a frente. A saída é alinhada para que a coluna “Date” represente os dados finais usados para gerar a previsão, de modo que “h.1” na linha “2020-05-29” seja a previsão da volatilidade condicional esperada de um dia à frente, feita usando dados até 29 de meio de 2020.

 

O gráfico hedgehog a seguir mostra os métodos de previsão ao longo do período analisado.
As linhas laranja indicam as previsões em diferentes intervalos de tempo.

 

 

#Visualização do gráfico hedgehog

g_previsões = resultados.hedgehog_plot()




Python Guide for Introductory Econometrics for Finance | Ran Tao & Chris Brooks
Value at Risk: Managing Financial Risk | Philippe Jorion
GARCH Models in Python | Chelsea Yang
Forecast volatility with GARH(1,1) | https://youtu.be/oDXw0r0Oqmk
Quandl Data to Python | https://www.quandl.com/tools/python

    


Link para visualizar a programação no Google Colab

https://colab.research.google.com/drive/1cDbLT0vHapiaOqT1ACrTnGfWTqb16xm6?usp=sharing


Posted by Andreza Menezes in Derivativos & Riscos, 4 comments
22
Jul
2020
RAPMs – Markowitz, CAPM e indicadores de risco e retorno

RAPMs – Markowitz, CAPM e indicadores de risco e retorno

RAPMs – Risk Adjusted Performance Measures – Parte 1
 
Diversos artigos do núcleo de Risco & Derivativos abordam a questão de gerenciamento de risco em um portfólio ou instituição. Neles, os membros do Clube de Finanças dissertam sobre métricas como o VaR (Value at Risk), os avanços do ES (Expected Shortfall), Risco de mercado, Princípios de Basileia e Teoria do Valor Extremo. Essas métricas são relacionadas às exposições das instituições financeiras em determinados ativos ou conjunto de ativos (portfólio), normalmente sob responsabilidade de um gestor de risco de mercado. Entretanto, métricas de risco podem ser utilizadas por outros profissionais no mercado financeiro com propósitos diferentes, como o gestor profissional de ativos ou o investidor pessoa física.

No livro Quantitative Methods in Finance (2008), a Profa. Carol Alexander coloca diferentes papéis para o gestor de risco de mercado e o gestor de ativos. O primeiro possui a necessidade de mensurar o risco de um portfólio frequentemente (e.g. diariamente) e não possui como principal preocupação o retorno desse conjunto de ativos. Por outro lado, o gestor de ativos tem como prioridade gerar retorno para seus investidores, assim como reportá-los e contextualizar os riscos envolvidos. Em um fundo de investimentos, por exemplo, essas duas variáveis são observadas em relação ao benchmark.
 
Tomando um fundo de investimentos como referência, caso um gestor considere somente o retorno de um ativo ou portfólio, uma parte excessiva do patrimônio seria alocada em ativos com retornos esperados (E(r)) acima da média, porém, possivelmente com riscos proporcionais. Sob outra perspectiva, caso o gestor considere somente o risco, pouco do patrimônio do fundo seria alocado neste(s) ativo(s).

O intuito do presente artigo é introduzir algumas métricas de risco utilizadas na gestão de ativos, mais precisamente indicadores de risco e retorno, conhecidos como Risk Adjusted Performance Measures (RAPMs).
 
Os primeiros RAPMs foram introduzidos no mercado financeiro durante a década de 60, juntamente com o Capital Asset Pricing Model (CAPM), originalmente proposto por William T. Sharpe (1964) e posteriormente por John Litner (1965). Visto que muitos RAPMs estão ligados ao CAPM, começaremos o artigo com uma revisão desse modelo, já citado em outras publicações do Clube de Finanças. 
O CAPM foi criado com base no trabalho de Harry Markowitz sobre diversificação e teoria moderna de portfólios, introduzida na década de 50. Apesar do tempo, esses trabalhos ainda são amplamente utilizados para estimativas de custo de capital e para avaliações da performance de gestão de portfólios, esse último, objeto deste artigo.
 
De forma breve, o modelo de escolha de portfólio desenvolvido por Markowitz (1959) presume que um investidor no tempo t-1 escolhe um portfólio que produz um retorno estocástico no tempo t. Como premissa, esse investidor é avesso ao risco e preocupa-se somente com a média e variância do retorno nesse período (entre t-1 e t). Nessa escolha, o investidor opta por um portfólio “média-variância-eficiente”, portanto, portfólios que i) minimizam a variância do retorno e ii) maximizam o retorno esperado, dada a variância do retorno.

Fonte: Fama and French (2004)

A figura acima demonstra a intersecção entre o trabalho de Markowitz e o desenvolvimento do CAPM.

 

O eixo horizontal do gráfico mostra o risco de determinado portfólio através do desvio padrão dos retornos e o eixo vertical demonstra o retorno esperado dos portfólios. Ao longo da curva abc, a qual é chamada de “fronteira de variância mínima” ou fronteira eficiente, é possível observar portfólios de ativos que minimizam a variância do retorno em diferentes níveis de retorno esperado, nesse primeiro momento com uma restrição em relação aos empréstimos com taxas livres de risco. No ponto T, por exemplo, o investidor que aceita volatilidade pode encontrar um portfólio com retorno esperado maior sem adicionar tanto risco (portfólios com maior desvio padrão). O ponto T pode ser interpretado como um portfólio “média-variância-eficiente”.

Ao retirarmos a restrição de empréstimos com taxas livres de risco, a fronteira eficiente torna-se uma linha reta, como a que passa pelos pontos Rf e g. Para entendimento dessa curva, podemos imaginar um fundo que investe uma proporção x de seu patrimônio em um ativo livre de risco (títulos do tesouro dos Estados Unidos, T-bills, por exemplo) e 1-x em um portfólio g. Se todo o patrimônio for direcionado para ativos livre de risco, o retorno esperado será o ponto Rf (taxa de juros livre de risco) no eixo vertical. Dessa forma, combinações entre ativos livres de risco e alocações em g formam a linha Rf-g. 

O portfólio g é uma dentre as infinitas combinações de ativos na curva abc e abaixo dela. Considerando a premissa de que o investidor opta por um portfólio ”média-variância-eficiente”, altera-se a inclinação da linha Rf-g até o ponto de tangência T, logo, nesse exemplo, os portfólios eficientes são combinações entre um ativo livre de risco e o portfólio T. Com um entendimento das distribuições dos retornos e a premissa de simetria de informações, os investidores tendem a optar pelo mesmo portfólio T, o qual os autores passam a denominar de M, em alusão ao “mercado”. 

A reta Rf-M é definida como a Capital Market Line (CML), a representação gráfica de diversos portfólios que otimizam combinações de risco e retorno, tanto em cenários de investimento (lend), como captação (borrow) à taxas de juros livres de risco.

Fonte: Alexander (2008)

Feitas as considerações acima, podemos entrar no conceito do CAPM e entender a sua relação com outras métricas que serão apresentadas. O modelo surge como uma forma de explicar o retorno dos ativos como um agregado de componentes do retorno. Tradicionalmente ele é utilizado em um contexto onde um ativo com risco, como por exemplo a ação de uma empresa, está prestes a ser adicionado à um portfólio diversificado e busca responder a seguinte questão: qual deveria ser o retorno adicional para justificar a inclusão deste ativo no portfólio diversificado?

Após a introdução do conceito podemos passar para a sua definição. Originalmente, o modelo CAPM Sharpe-Lintner foi baseado no conceito de equilíbrio de mercado, onde o excesso de retorno esperado de um ativo i (E(Ri) – Rf) seria proporcional ao retorno adicional do mercado (E(Rm)-Rf), aqui citado como o portfólio M.

Equação 1:


Com base na fórmula acima e uma pequena manipulação algébrica, o retorno esperado de um ativo i é a taxa livre de risco Rf, mais um prêmio pelo risco, o qual é definido pelo Beta do ativo i (beta i) multiplicado pelo prêmio por unidade de “risco beta”, E(Rm) – Rf.

Na equação apresentada, o Beta do ativo i é a covariância dos retornos do ativo i e do mercado divididos pela variância do retorno do mercado. Na prática, ele pode ser calculado através de uma regressão linear simples dos retornos do ativo contra os retornos do mercado. O beta será o coeficiente angular da reta de regressão.

 Equação 2:

Ao pensar em um modelo de regressão para estimar o retorno esperado de um ativo, podemos chegar na seguinte equação: 

Equação 3:

 

Onde os componentes da equação continuam com o mesmo significado, porém, o retorno de determinado ativo não é explicado totalmente pelo excesso de retorno do mercado, surge um termo de erro aleatório ẽ. 

Para facilitar o entendimento das métricas que serão apresentadas, faremos uma alteração no CAPM Sharpe-Lintner. Como já foi comentado, as equações 1 e 3 podem ser eficientes para responder a principal questão do CAPM e por consequência estimar o risco sistemático de um ativo individual ou um de um portfólio não gerenciado ativamente. Porém, ao aplicar essa fórmula para um portfólio gerido ativamente, o gestor pode selecionar ativos com um ẽ significativamente maior do que zero, em função de habilidades ou conhecimentos que não estão disseminados no mercado. Com isso, o portfólio não será explicado somente pelo seu beta, o que é plausível em um contexto onde existe um gestor de ativos, portanto, um ponto falho do CAPM Sharpe-Lintner.

Em estudos posteriores, autores como Jensen (1968),  Douglas (1968), Black, Jensen & Scholes (1972), Fama & MacBeth (1973) e Fama & French (1992), encontraram que o intercepto da equação do CAPM é consistentemente maior do que a taxa livre de risco Rf. Além disso, as regressões mostraram que, em média, o prêmio por unidade de “risco beta”, é consistentemente menor do que o excesso de retorno do mercado em relação à taxa livre de risco, E(Rm) – Rf. Dessa forma, para facilitar o entendimento dos próximos tópicos do artigo, adotaremos a equação proposta por Jensen em seu trabalho de análise de performance de fundos mútuos.

 Equação 4:

Onde o intercepto 𝛼 (alpha) pode ser entendido, segundo Jensen, como o retorno médio incremental no portfólio devido à habilidade do gestor de ativos. De outra forma, é possível definir o 𝛼, posteriormente denominado de alpha de Jensen, como o retorno do portfólio não explicado diretamente pelo retorno adicional do mercado em relação ao ativo livre de risco, E(Rm) – Rf.

RAPMs baseados no CAPM

Nessa parte do artigo apresentaremos os RAPMs que surgiram concomitantemente com o CAPM, logo, fazem referência ao modelo. Esses RAPMs introdutórios podem ser utilizados para rankeamento de portfólios por uma ordem de preferência, de acordo com as intenções do investidor ou gestor de ativos. 

Sharpe Ratio 

O Sharpe Ratio foi desenvolvido por WIlliam F. Sharpe e assim como os outros RAPMs leva em conta o retorno de um ativo em relação ao risco. O indicador é interpretado como o excesso de retorno de um ativo em relação ao ativo livre de risco, por unidade de volatilidade (𝜎 desvio padrão).

Aqui, fazemos a primeira referência à parte introdutória do artigo. O Sharpe Ratio é a inclinação da Capital Market Line (CML), portanto, quanto o retorno esperado do ativo ou portfólio aumenta/diminui com mudanças na volatilidade (𝜎 desvio padrão). De forma breve, portfólios com Sharpe ratios maiores tendem a ser priorizados por investidores e gestores de ativos em um rankeamento. É importante pontuar que, ao considerar o E(R) do ativo, presume-se que os retornos sejam normalmente distribuídos, o que muitas vezes não acontece na prática.

Fonte: Alexander (2008)

Treynor Ratio
Supondo a existência de um 𝛼 (vide equação 3) nos retornos de um ativo/portfólio com risco, sob a ótica do CAPM, Treynor propôs um indicador associado à esse retorno não correlacionado com o mercado.

O Treynor Ratio possibilita ordenar portfólios de acordo com os retornos não explicados pelos retornos de mercado, por unidades de risco sistemático (Beta).
 
Information Ratio ou Appraisal Ratio

O appraisal ratio possui suas origens na teoria proposta por RIchard Grinold e aprofundada por Clarke, de Silva e Thorley sobre a Law of Active Management, a qual busca conceituar o valor adicionado pelos gestores de ativos/portfólios. O appraisal ratio foi criado com o objetivo de mensurar e distinguir as habilidades dos gestores de ativos.

Como é possível observar na fórmula acima, gestores de portfólios com retornos ativos (𝛼) por unidade de risco (𝜎 desvio padrão), possuem um appraisal ratio maior.

Limitações

O CAPM tem sido utilizado de forma ampla desde a década de 60 até os dias atuais e diversas adaptações foram feitas ao modelo, como é possível observar na equação 4 e nos estudos de Jensen (1968),  Douglas (1968), Black, Jensen & Scholes (1972), Fama & MacBeth (1973) e Fama & French (1992) citados anteriormente. Mesmo com a utilização frequente do CAPM, faz-se necessário entender as suas limitações e rigidez nas premissas. 

O CAPM Sharpe-Lintner define que o prêmio de risco esperado por um ativo está relacionado somente com o seu risco sistemático, ou seja, a sua relação com o retorno adicional de um portfólio de mercado (E(Rm) – Rf). Conforme comentado anteriormente, em outros estudos foi possível rejeitar estatisticamente que o prêmio por unidade de “risco beta”, é consistentemente menor do que o excesso de retorno do mercado em relação à taxa livre de risco, E(Rm) – Rf, assim como o intercepto é maior do que o retorno de um ativo livre de risco Rf. Uma alternativa ao modelo CAPM Sharpe-Lintner já foi discutida anteriormente em um artigo do Clube de Finanças. Ao considerar outras variáveis além do retorno do mercado, o modelo de 3 fatores de Fama e French surge como uma alternativa para a precificação de ativos.

Quanto às premissas, o modelo pressupõe que: (1) todos os investidores possuem utilidades de maximização de riqueza, em um período, avessas ao risco e podem escolher diferentes portfólios somente em função de suas médias e variâncias, (2) não existem impostos e custos de transação, (3) todos os investidores têm visões homogêneas sobre os parâmetros da distribuição conjunta de probabilidade dos retornos dos ativos/portfólios e (4) os investidores podem emprestar e tomar emprestado a uma taxa livre de risco. Dessa maneira, podemos perceber que existe certa rigidez nas premissas e na formatação do modelo ao considerar, por exemplo, que o retorno adicional de um ativo é explicado somente pelo retorno do mercado ou que todos os investidores possuem visões homogêneas sobre o comportamento da distribuição de retorno de um ativo.

Parte 2
 
Na parte dois falaremos sobre o Kappa, Omega e Sortino Ratios, assim como traremos algumas aplicações práticas desses índices.
 
> Referências

Jensen, Michael C., The Performance of Mutual Funds in the Period 1945-1964. Journal of Finance, Vol. 23, No. 2, pp. 389-416, 1967.

Vidyamurthy, Ganapathy. Pairs trading : quantitative methods and analysis. Hoboken, N.J.: J. Wiley, 2004.

Jensen, Michael C. and Black, Fischer and Scholes, Myron S., The Capital Asset Pricing Model: Some Empirical Tests. Praeger Publishers Inc., 1972.

Alexander, Carol. “Market Risk Analysis, Quantitative methods in finance”. John Wiley & Sons, 2008.

Leibowitz, Martin L. Modern portfolio management: active long/short 130/30 equity strategies, 2009.

Sharpe, William F. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, The Journal of Finance, Vol. 19, No. 3, 1964.

Fama, Eugene F. and French, Kenneth R. The Capital Asset Pricing Model: Theory and Evidence, Journal of Economic Perspectives, Volume 18, Number 3, 2004.

Posted by Thiago Ranzolin Barreto in Derivativos & Riscos, Equity Research, 0 comments
13
Jul
2020
Stress Testing Financeiro

Stress Testing Financeiro

No controle de riscos, medidas estatísticas como o VAR e o beta nos ajudam a estabelecer as probabilidades do comportamento de um portfólio diante de condições esperadas, baseando-se em dados históricos. Contudo, nem sempre os eventos do mercado ocorrem de maneira previsível. Certas vezes, a movimentação é tão brusca que sua chance de ocorrer seria quase nula em uma distribuição de retornos normal, mas sabemos, através das diversas crises mundiais das últimas décadas, que esses eventos são muito mais prováveis do que a curva nos mostra. Em virtude disso, faz-se necessário a existência de um método para controlar o risco nas situações de perdas extremas. Esse método é o stress test.

Um teste de estresse financeiro é um modelo não estatístico de controle de riscos que utiliza a simulação computacional para testar um portfólio sob mudanças bruscas e improváveis em fatores determinantes para o valor da carteira. O método é considerado não estatístico porque ele não busca estabelecer a probabilidade das perdas, ele apenas reconhece que essas perdas são possíveis e foca no impacto gerado caso elas ocorram. Desse modo, o gestor pode identificar vulnerabilidades que não seriam detectadas nos cenários base previstos e tomar medidas de hedge contra os cenários que ele considerar importante estar protegido.

Entre esses cenários, através de uma análise daquilo que é relevante para o negócio, o gestor deve observar para quais situações a empresa quer estar preparada e para quais não vale a pena se preocupar. Entre os possíveis eventos, o gestor pode querer se proteger de, por exemplo, um tsunami no Japão, um terremoto nos Estados Unidos, uma guerra na região do Golfo Pérsico ou uma pandemia global.

Ademais, observando as movimentações do mercado em resposta a crise do coronavírus, temos um caso prático da importância do stress test, já que, apenas no mês março de 2020, tivemos 6 movimentações que excederam 10% no índice Bovespa, valor sete vezes maior que o desvio padrão dos movimentos dos últimos 10 anos. Tal baixa no índice levou muitos fundos a exibirem quedas catastróficas no valor de suas cotas, e aqueles que possuíam uma proteção contra os cenários adversos conseguiram controlar essas perdas.

COMO É APLICADO NO MUNDO?

Companhias que gerenciam ativos e investimentos usam os testes de estresse regularmente para controlar o risco de suas carteiras e, a partir disso, tomar as decisões necessárias para mitigar possíveis perdas. Além de ser utilizado na tomada de decisão de grandes gestoras, projetos de empresas e bancos, os testes de estresse tornaram-se obrigatórios no controle mundial de riscos e passaram a ser exigidos dos bancos que desejam atuar internacionalmente, além da legislação local de certos países que exigirá os testes dependendo do tamanho da instituição. Nesse sentido, as crises mundiais recentes trouxeram à tona o risco excessivo ao qual as instituições financeiras estavam se submetendo e a regulamentação passou a evoluir de acordo.

Após a crise de 2008, novas normas regulatórias surgiram com foco em *stress testing *e adequação de capital, dentre elas temos o Dodd-Frank Act de 2010, que está em vigor até hoje. A norma impõe o uso de testes de estresse na estrutura de capital dos bancos estadunidenses e os cenários de teste são estabelecidos pelo corpo regulatório do FED e supervisionados por comitês independentes. O Federal Reserve gera três cenários – um otimista, um pessimista e um extremamente pessimista – e as instituições devem exibir planos de resposta aos três. Além disso, é pedido que os bancos gerem seus próprios cenários para garantir o controle de riscos individual que não consta nos cenários estabelecidos pelo FED.

Essas regras afetam, pela análise do Comitê de Estabilidade Financeira feita em 2018, 22 bancos mundiais considerados *too big to *fail. Essa lista incorpora os bancos com atuação ao redor do globo que gerenciam mais de U$50bi em ativos.

Dado o conceito do stress test como uma ferramenta complementar no controle de riscos e sua aplicação no contexto mundial, entraremos em detalhes em alguns dos modelos.

MODELOS DE ANÁLISE DE CENÁRIO

Um teste de estresse é composto de três etapas fundamentais: a primeira sendo a definição de um cenário, a segunda a modelagem dos fatores desse cenário e a última o estabelecimento de políticas de resposta baseadas nos dados obtidos.

Tratando da primeira fase de um stress test, existem duas aproximações possíveis, que são definir um cenário hipotético ou basear-se em um cenário histórico de uma crise passada. A vantagem deste é que não é preciso pensar em problemas como a correlação entre fatores no seu cenário – ou seja, toda a segunda etapa do teste se torna imediata – uma vez que, como o evento já ocorreu, o gestor possui todos os dados e variações de preço e índices da época. Por causa disso, o método histórico é mais simples de aplicar o que o torna muito utilizado.

A outra maneira de se definir um cenário é estudar o portfólio, buscando entender quais fatores de risco mais o afetam e gerar um cenário no qual esse fatores seriam negativamente impactados. A partir disso, é possível ter o controle de risco para um cenário possível específico que seria desastroso para a empresa, mas que ainda não está nos livros históricos. O grande problema desse método é saber como tratar as diversas variáveis se movimentando em todas as direções. Afinal, mesmo em um cenário extremo, não se espera que todos os fatores se desloquem na direção mais negativa à carteira, graças a correlação. Buscando resolver esse problema, o analista pode usar os seguintes modelos:

Cenários Unidimensionais

  • Testes de Sensibilidade – são a metodologia tradicional de análise de cenários e focam em apenas uma variável, anulando assim o problema da correlação multidimensional. Os testes mais comuns envolvem movimentações em um único dia de fatores fundamentais, como uma movimentação de 1% na curva de juros, uma alta de 20% na volatilidade implícita, quedas ou altas de 10% no índice da bolsa ou alteração de 20% no câmbio da moeda local contra o dólar.

Cenários Multidimensionais

  • Método da Movimentação de Variáveis – é um modelo extremamente conservador, no qual movimenta-se diversos fatores para cima e para baixo em um certo número de desvios padrão. Feito isso, busca-se a combinação de movimentos que geraria o pior resultado possível ao valor da carteira e assume-se este como o resultado do stress test. Como comentado anteriormente, essa combinação, por desconsiderar a correlação, faz com que as perdas observadas sejam muito maiores do que em um cenário real.
  • Método de Cenários Condicionais – possui uma elaboração sistemática que incorpora a correlação entre as variáveis. Para isso, considera-se dois conjuntos, um conjunto R* composto por variáveis chave sujeitas a movimentos extremos, que serão dados pelo cenário estabelecido, e outro conjunto R composto das demais variáveis, que não está sujeito a nenhuma movimentação inicial. A partir disso, faz-se uma regressão das variáveis R nas variáveis R* e obtemos a variação de R a partir do cenário hipotetizado, através da correlação. Desse modo, conseguimos avaliar o portfólio antes e depois, contudo, essa análise dependerá de uma boa escolha pelo gestor das variáveis chave (R*) e das demais (R), o que sempre parte do entendimento da carteira em questão.

STRESS TESTING APLICADO

Agora que entendemos as metodologias para os testes de estresse, estaremos aplicando o conceito para o risco de uma carteira hipotética nos principais dias de perdas durante a atual crise do coronavírus. Isso implica que estaremos utilizando o método histórico, já que todas as movimentações já são conhecidas.

Abaixo, temos a posição de nossa carteira hipotética, divida entre Ações, moeda, bolsa internacional e títulos públicos:

A partir disso, vamos testar essa carteira nas maiores perdas ocorridas na bolsa brasileira durante a crise, ocorridas nos dias 9, 12, 16 e 18 de março com quedas no índice de 12,5%, 15%, 14,9% e 10,9% respectivamente. Testando o portfólio mencionado nesses dias, a carteira apresentou os seguintes resultados:

Nota: Ativo representa a variação percentual do ativo no dia, PP representa o efeito que o ativo teve na variação do portfólio e Total é a soma das variações ponderadas dos ativos, o resultado do portfólio no dia.

Observa-se que a carteira teve uma performance bem superior ao Bovespa, devido a diversificação em ativos de crise como o dólar e o ouro e a posição em renda fixa. Contudo, se compararmos o resultado do portfólio com o VaR esperado dessa carteira de -0,98% com 99% de certeza, vemos que as perdas excederam muito o esperado em todos os dias. Além disso, o desvio padrão dos retornos da carteira foi de 0,42%, ou seja, nos dias da crise, as perdas variaram de dez a até quase vinte vezes o desvio padrão.

Partindo de uma distribuição normal para calcular a probabilidade do ocorrido, calcula-se que o evento do dia 9 de março – que é o mais otimista dentre as possibilidades – deveria ocorrer uma vez a cada 360 bilhões de bilhões de anos. Não é preciso dizer que qualquer gestor sensato atribuiria uma chance muito maior de ocorrer uma pandemia global do que os retornos da curva normal tentam nos dizer. Essa chance continuaria não sendo muito alta, porém, com o stress test, é possível ter uma ideia do que aconteceria e tomar as medidas de hedge necessárias.

Por fim, concluída a parte matemática de um teste estresse, vamos para a última etapa, as políticas de resposta.

POLÍTICAS DE RESPOSTA

Realizados todos os cálculos do teste, a pergunta que surge é o quê fazer caso o tamanho das perdas esperadas seja grande de mais. Em muitos casos, os resultados de um teste são tão catastróficos que eles passam a ser ignorados e tomados como irrelevantes. É claro que empresa alguma consegue estar preparada para lidar com os infinitos cenários que o mundo pode oferecer. Porém, existem cenários relevantes e possíveis para cada setor que devem ser considerados para tomar medidas de resposta. Posto isso e como colocado já anteriormente, a escolha dos eventos deve partir da experiência prévia da gestão, elencando situações que mais fazem sentido e são potencialmente prejudiciais à firma.

Estabelecidas as posições que a empresa quer proteger, existem inúmeras medidas que podem ser tomadas pelo gestor para se proteger dos cenários, entre elas:

  • Acúmulo de capital suficiente para pagar o prejuízo possível;
  • Comprar proteção de seguros para os eventos analisados;
  • Modificar o portfólio buscando reduzir o impacto de um evento específico, reduzindo a exposição ao risco ou diversificando através de ativos;
  • Reestruturar o negócio ou o produto buscando melhor diversificação;
  • Desenvolver um plano de ações para caso o cenário comece a se desenvolver;
  • Preparar fontes de financiamento alternativas caso a liquidez do portfólio comece a cair.

Dessa forma, conclui-se todas as etapas da metodologia do stress test. Vimos que o teste de estresse é um instrumento não estatístico para controle de riscos e tratamos de exemplos práticos de como ele complementa o Value at Risk, que falha em captar perdas muito acima do normal. Além disso, mostramos que esse plano para situações adversas tem o papel fundamental de garantir a sobrevivência da instituição aos cenários elencados.


REFERÊNCIAS

JORION, Philippe. Financial Risk Manager Handbook. 3. ed. New Jersey: John Wiley & Sons Inc, 2007. p. 241-264
JORION, Philippe. Portfolio Risk: Analytical Methods. Value At Risk: The New Benchmark for Managing Financial Risk. 3. ed. New York: Mcgraw Hill Companies, 2007. p. 357-377
Key Points From the 2015 Comprehensive Capital Analysis and Review (CCAR). Harvard Law School, 22 de março de 2015. Disponível em: https://corpgov.law.harvard.edu/2015/03/22/key-points-from-the-2015-comprehensive-capital-analysis-and-review-ccar. Acesso em: 15 de abril de 2020.
Comprehensive Capital Analysisand Review 2015:Assessment Framework and Results, março de 2015. Disponível em: https://www.federalreserve.gov/newsevents/pressreleases/files/bcreg20150311a1.pdf. Acesso em: 15 de abril de 2020.

Posted by Leonardo de Sá Nicolazzi in Derivativos & Riscos, 3 comments
07
Jul
2020
Introdução à Corporate Finance

Introdução à Corporate Finance

Corporate Finance (Finanças corporativas) é o nome dado a divisão das finanças que lida com situações como: fontes de financiamento, estruturação de capital e decisões de investimento. A principal preocupação aqui, na Corporate, é maximizar o valor do acionista nas decisões, tanto de curto como de longo prazo, da companhia.

Uma das principais atribuições dada aos departamentos de Finanças Corporativas é o de investimento. Não só administrar e supervisionar, mas tomar decisões que façam sentido dado o momento e o segmento da firma. Como por exemplo, podemos citar um empreendimento realizado por uma empresa de Real State. A firma sabe que precisa fazer algum projeto que rentabilize seu capital. Cabe então ao departamento de Corporate não só analisar as melhores oportunidades, mas também a estratégia a se seguir. Algumas perguntas a serem feitas em relação a estratégia: Qual investimento devo fazer? Qual investimento maximizara meu retorno? Devo fazer com capital próprio, de terceiros ou através de Equity?

Dentro das Finanças Corporativas, há uma série de instrumentos usados para calcular a viabilidade de um projeto ou investimento. Passaremos por todos, citando exemplos e suas respectivas fórmulas com o uso na HP 12C. Antes de tudo, é importante ressaltar que aqui lidaremos com o assunto de Finanças Corporativas, o que envolve o uso de matemática financeira. Iremos apresentar os termos, fórmulas e explicar cada um. Logo após, faremos um resumo de como deve ser tomada a decisão de um investimento e suas implicações, para isso, usaremos exemplos numéricos com o uso da HP12C.

Future Value e Present Value

Começando com Future Value (Valor futuro), que chamaremos de FV. O FV de um número nada mais é do um montante de dinheiro hoje, avaliado em um dado ponto do futuro. Já o Present Value (Valor Presente), é o próprio montante avaliado hoje. Podemos usar uma fórmula para ambos os termos:

  • FV = Future Value
  • PV = Presente Value
  • R = Taxa de juros ou Custo de Capital

Assim, temos que o FV é o PV multiplicado por 1 mais o custo de capital do investimento, elevado ao número de anos da duração do investimento ou projeto. Para acharmos o PV quando tivermos o FV, basta reorganizar os termos da equação para isolar o PV.

Net Present Value (NPV) ou Valor Presente Líquido (VPL)

Agora, entrando a fundo no conceito de Corporate, começaremos a aplicar funções mais úteis. Iniciando pelo Net Present Value (Valor Presente Líquido, VPL) que chamaremos de NPV. O NPV é muito utilizado para fazer valuation (estimar o valor econômico de algo, nesse caso um projeto/investimento) para se obter uma ideia da viabilidade do projeto. De forma resumida, o NPV é o valor presente de todos os fluxos de caixa que estão relacionados ao projeto. É dado pela fórmula:

  • NPV = Net Presente Value
  • CF0 = Investimento
  • CFt = Fluxo de Caixa no período t

É interessante ressaltar que o Investimento entrará com sinal negativo, visto que há uma saída de caixa, não uma entrada.

Perpetuity (Perpetuidade)

Para seguirmos, tem-se o conceito de Perpetuity (Perpetuidade), que tem como premissa o investimento feito que durará infinitamente e os fluxos de caixa serão sempre os mesmos:

  • C = Fluxo de caixa
  • R = taxa

Já se supusermos que os fluxos de caixa não serão constantes, mas sim crescerão a uma taxa (g), temos que:

  • G = growth, taxa de crescimento

Annuity (Anuidade)

O último conceito para fluxo de caixa é o de Annuity (Anuidade), que consiste em um fluxo de caixa fixo recebido constantemente por um certo período:

Internal Rate of Return (IRR) ou Taxa Interna de Retorno (TIR)

Entrando no tema Rentabilidade, temos alguns conceitos a serem abordados. O Internal Rate of Return (Taxa Interna de Retorno), ou IRR, é a rentabilidade a ser adquirida para que o NPV seja 0, ou seja, para que o projeto seja sustentável. Temos como fórmula para o IRR:

Payback

Outro termo que vamos comentar já é bem disseminado pelo mercado em geral e é conhecido como Payback. Nada mais é o tempo em anos para a recuperação do valor investido. É fácil notar que, tudo o mais constante, o projeto com o menor payback deve ser escolhido, pois haverá o retorno financeiro mais cedo.

Profitability Index (Índice de Rentabilidade)

Já o Profitability Index é basicamente a rentabilidade do investimento e é dado por:

Quando realizar ou não um investimento?

Dado todos os índices e fórmulas dadas, podemos agora fazer a aplicação na HP12C. Porém, antes disso, é interessante que se decida quando e porque fazer o investimento. De nada adianta calcular todos os índices, se não se sabe qual decisão tomar e nem o motivo.

Então, começando pelo NPV temos que o investimento/projeto deve ser feito quando o NPV>0, ou seja, positivo. Deve-se, em teoria, aceitar todos os investimentos que tiverem um NPV acima de 0, porém na prática a empresa não possui recursos ilimitados e por muitas vezes há um limite de capital disponível para ser usado. Quando há tal restrição, deve-se fazer o investimento no qual tiver o maior NPV, visto que o valor presente de tal projeto terá um valor presente maior que os demais.

Já levando em conta o IRR, deve-se aceitar todos os projetos no qual o IRR for maior que o custo de capital da empresa. Porém, ao ter de escolher investimentos excludentes, é interessante que se escolha o maior IRR possível, pois a rentabilidade será mais alta.

Há também um outro empecilho: o desacordo entre NPV e IRR, visto que ao termos 2 investimentos a serem feitos e calculados ambos os índices, um pode obter o IRR maior e o outro o NPV maior. Nesse sentido, deve-se sempre optar pelo qual possuir o maior NPV, pois o IRR não leva em conta a ordem dos fluxos de caixa. Por exemplo, o projeto A possui um investimento de 1000, o fluxo de caixa 1 de 500 e o fluxo de caixa 2 de 1000. Já o projeto B possui o contrário, com investimento de 1000, fluxo de caixa 1 de 1000 e fluxo de caixa 2 de 500. Ambos irão possuir o mesmo IRR, porém o projeto B terá um NPV maior, por conta de receber o maior fluxo de caixa primeiro. Logo, a escolha que maximizará o retorno é o projeto B.

Aplicação na HP12C

Agora que foi visto todos os componentes de estudo da Corporate Finance, podemos partir para exemplos práticos e utilizando a HP12C.

Exemplo 1: Dado um montante de R$1230 hoje, rendendo a uma taxa de 0.5% ao mês por 6 anos, qual o montante gerado ao final do período?

Resposta: Antes de tudo, limpar a memória usando f e CLx. Clicar em: 1230, depois em CHS (esse botão faz com que o sinal do input seja negativo, visto que é uma saída de caixa) e logo após em PV, pois esse é o valor do aporte. Depois, clicar em 0.5 e na tecla i, logo após, clicar em 72 (6 anos e meses) e em n. Todos os inputs feitos, clicar em FV para obter o resultado ao final do período, que será de R$1761,41.

Exemplo 2: Uma empresa investiu 15.000 reais em uma fábrica que irá retornar os seguintes fluxos de caixas nos próximos anos: 8.000, 6000, 4500, 2000. Calcular o NPV sabendo que o custo de capital da firma é de 12%.

Resposta: Para fazermos na HP12C, começar pelo investimento. Clicar em 15000, CHS, g (opção “azul” para fluxo de caixa) e em PV. Após isso, começaremos a colocar os próximos fluxos de caixa. 8000, g e PMT para a HP12C entender que é um fluxo de caixa no período 1. 6000, g e PMT. 4500, g e PMT e, por fim, 2000, g e PMT. Feito os fluxos de caixa, clicar em 12 e em i para o custo de capital e em f e PV para obter o NPV do projeto, que nesse exemplo é de 1400. Sendo positivo, o investimento é qualificado como viável.

Exemplo 3: Usando o exemplo interior, como podemos obter o IRR?

Resposta: Podemos fazer o mesmo procedimento anterior, porém não colocamos o i e em vez de clicar em f e depois em PV para obter o NPV, clicamos em FV para obter o IRR. Como resultado, temos: 17.41%, o qual é maior que o custo de capital da firma.

Exemplo 4: Também usando o exemplo dado, temos que a rentabilidade é de?

Resposta: Clicar em 8000, ENTER, 6000, ENTER, 4500, ENTER, 2000 e em + três vezes, pois foram feitas 4 somas. Clicar em ENTER, 15000 e no símbolo de dividir. Obtêm-se o resultado de 1,37, ou 137% de rentabilidade.

Exemplo 5: Usando os fluxos de caixas anteriores, qual o payback do projeto?

Resposta: Como nesse caso os fluxos de caixa não são constante, há de se usar o payback modificado. Para isso, somamos os fluxos de caixa até obtermos o resultado mais próximo do investimento. Por exemplo, é fácil notar que o payback é algo entre o segundo e o terceiro fluxo de caixa, visto que os dois primeiros fluxos somam 14000, número próximo de 15000. Visto isso, sabemos que o Payback é 2,XX. Para descobrir o XX, temos de pegar o restante para o retorno do investimento (1000) e dividir pelo próximo fluxo de caixa. Tem-se então: 0,22. Somado com os 2 outros fluxos, tem se o payback desse projeto de 2,22 anos.

Posted by Davi Jahn in Equity Research, 0 comments
01
Jul
2020
VaR Tools

VaR Tools

Risco em Portfólio: Métodos Análiticos

No artigo, Value At Risk, foi introduzido o conceito por trás dessa medida de risco e foram abordados conceitos como origem, técnicas de estimação e até mesmo suas deficiências. Neste artigo, iremos trabalhar em cima dessa medida trazendo o conceito e aplicação de outras ferramentas que permitem gestores controlarem melhor os riscos de um portfólio.

Essas ferramentas, denominadas VaR Tools, são essenciais para que os investidores possam identificar os ativos que mais contribuem para o risco total de uma carteira. Também, são usadas para chegar no melhor hedge da carteira, e selecionar os ativos de risco alinhados com melhores retornos.

Portfólio

Em termos gerais, um portfólio é caracterizado como um conjunto de aplicações do investidor, que reúne todos os ativos financeiros escolhidos para realizar investimentos. Esse portfólio permite a diversificação de ativos bem como a minimização de riscos, trazendo mais ganhos ao investidor e menos volatilidade do capital. E se as posições desse portfólio são fixadas durante um período, a taxa de retorno do portfólio é uma combinação linear dos retornos dos ativos subjacentes, onde os pesos são dados pelos montantes investidos no começo do período.

A taxa de retorno do portfólio de t para t + 1 pode ser definida como:

\[ R_{p,t+1}=\sum_i^Nw_{i}R_{i,t+1} \]

Sabendo que N é o número de ativos \(R_{i,t+1}\), é a taxa de retorno do ativo i, e \(w_{i}\) é o peso do ativo.

VaR Tools

O Value At Risk, inicialmente, foi desenvolvido como uma medida para mensurar o risco de um portfólio. Porém, há muito mais por trás do VaR do que uma mensuração de um simples número.

Com o tempo, os gestores puderam encontrar maneiras de usar o VaR para realmente gerir riscos, e foi levantado a pergunta: “Que posições eu devo alterar na minha carteira, para que o VaR seja mais eficiente?”

Para responder a esta pergunta, entramos no propósito deste artigo: as VaR Tools, que incluem a marginal, a incremental e a componente.

Marginal VaR

Os VaRs individuais dos ativos são ineficientes para mensurar as mudanças de posições em portfólios, por conta que eles não levam os poderes da diversificação. O que realmente importa é o VaR individual de cada ativo levando em conta a diversificação, que pode ser encontrado através das VaR Tools.

Tendo em vista a ineficiência do VaR individual dos ativos na mensuração de mudanças de posições num portfólio e a volatilidade no retorno de um ativo, passa-se a analisar a contribuição dele para o risco do portfólio utilizando o Marginal VaR.

Um portfólio hipotético existente, é feito com um número N de ativos numerados de j = 1, …, N. Esse portfólio é alterado quando adicionamos uma nova unidade de um ativo i. E para ter conhecimento do impacto dessa adição de unidade, pode ser calculado a contribuição “marginal” do risco.

Essa contribuição marginal, chamada de Marginal VaR, habilita os gestores de riscos a estudarem os efeitos da adição ou subtração de posições de investimento em um portfólio.

E dado que o VaR é afetado pela correlação dos ativos, não é suficiente considerar os ativos individualmente. Eles devem ser comparados com o portfólio total para determinar a contribuição real.

Em teoria, podemos explicar o marginal VaR como a mudança no portfólio VaR resultado da adição de uma unidade de um certo componente.

Colocando em fórmulas, podemos correlacionar o marginal VaR \(\triangle VAR_{i}\) e o Beta \(\beta\), que mede a contribuição de um ativo para o risco total do portfólio, como:

\[ \triangle VaR_{i}=\frac{∂VAR}{∂x_{i}}=\alpha(\beta_{i}\sigma_{p})=\frac{VAR}{W}x\beta_{i} \]

O marginal VaR pode ser usado com diferentes formas e propósitos de gerenciamento de risco. Pode-se supor, como exemplo, que um investidor tenha uma carteira com diferentes tipos de ativos e ele deseje reduzir o VaR. Ele pode ranquear todos os marginais VaRs e pegar aquele com maior \triangle VAR porque será o que trará o maior efeito de hedging.

Incremental VaR

A metodologia do marginal var pode ser estendida para calcular o total impacto de uma mudança em um portfólio p. Um novo trade é realizado, agora através da adição de uma posição a.

Deve ser medida a adição deste novo trade, para chegar no incremental var, através da medição do VaR do portfólio inicial \(VAR_{p}\) juntamente com o cálculo do VaR com a nova posição \(VAR_{p+a}\). O var incremental é obtido usando a fórmula abaixo:

\[ Incremental VaR=VaR_{p+a}- VaR_{p}\]

Esse antes e depois é bastante informativo. Se o VaR diminuir, estamos fazendo um hedging, ou redução de risco, se o VaR aumentar estamos aumentando o risco.

Um grande ponto dessa técnica é que ela requer uma reavaliação total do novo portfólio VaR com o novo trade a. E isso pode ser bastante difícil para grandes portfólios, por que pode demorar para calcular o novo VaR.

Mas, caso o gestor prefira uma melhor aproximação do resultado real para poupar tempo de computação, pode-se tomar um atalho. O Incremental VaR é capaz de ser calculado utilizando-se do marginal VaR:

\[ Incremental VaR=(∆VaR)` α\]

Então estaríamos trocando um tempo de computação por uma acurácia menor.

Componente VaR

Outra VaR Tool extremamente necessária para a gestão de risco é a Component VaR.

Ao invés disso, precisamos de um aditivo de decomposição do VaR que reconhece os poderes de diversificação. E, por isso, utilizamos a marginal VaR como uma ferramenta para medir a contribuição de risco de cada ativo existente no portfólio.

\[ Component VaR=(∆VaR)` w_i W\]

O Component VaR indica quanto do portfólio VaR irá se alterar, aproximadamente, caso um componente seja removido do portfólio. Os componentes do VaR adicionados juntos dão o valor do portfólio total:

\[ VaR=CVaR_1+ CVaR_2+⋯+ CVaR_N=VaR\sum_{i=1}^Nw_i β_i)\]

O cálculo pode ser simplificado tomando em consideração que \(\beta_{i}\) é igual a correlação \(\rho\) vezes o desvio padrão do ativo \(\sigma_{i}\) dividido pelo desvio padrão do portfólio \(\sigma_{p}\).

\[ CVaR_i=VaRw_{i}β_i= VaR_iρ_i\]

Sumarização das VaR Tools

O gráfico abaixo, traz uma sumarização das VaR Tools. Na posição de 1 milhão, o VaR do portfólio é de $257.738. O Marginal VaR é a mudança no VaR devido a adição de $1 em euro. Isso é representado pela inclinação da linha reta que é tangente ao VaR da curva.

O Incremental VaR é a mudança no VaR devido a eliminação da posição em euro, que é de $92,738 e medido ao longo da curva. Isso é aproximado com o Componente VaR, que é simplesmente o marginal VaR vezes a posição corrente de 1 milhão, ou $152,108.

O gráfico também mostra que a posição de melhor hedge seria com uma posição zero em euro. Essas mudanças podem ser todas vistas através da tabela abaixo:

A screenshot of a cell phone Description automatically generated

Esta tabela além de sumarizar o gráfico também traz a importância do uso do Marginal VaR e Component VaR. A coluna da marginal VaR pode ser usada para determinar como diminuir o risco. Dado que o marginal VaR do euro é superior ao do dólar canadense, cortar a posição em euro pode ser muito mais efetivo do que cortar a posição em dólar canadense.

Mnimização de Risco de Portfólio

Para minimizações de risco em portfólio, as posições devem ser cortadas onde o marginal VaR é o maior, assim se mantém um portfólio adequado. Se um portfólio está com risco alto e precisa ser reinvestido, as posições que apresentarem menor marginal VaR podem ser adicionadas para fazer as primeiras mudanças.

Esse processo pode ser repetido até o ponto que o portfólio chegar no risco mínimo, nesse ponto todos os VaR marginais e os betas dos portfólios devem ser iguais:

\[ ∆VaR_i= VaR\div Wβ_i=constante\]

A tabela abaixo ilustra esse processo com duas posições em um portfólio. A posição original é $2 milhões em dólares canadenses e $1 milhão em euro, gerando um VaR de $257,738, ou volatilidade do portfólio de 15,62 por cento. O marginal VaR do euro é de 0.1521, que é maior do que o do dólar canadense.

A screenshot of a cell phone Description automatically generated

Como resultado, a posição em euro deve ser cortada adicionando posição em dólar canadense. A tabela mostra, a posição final com o risco diminuído. O peso do euro foi diminuído de 33,33 para 14,79 por cento. A volatilidade do portfólio foi diminuída de 15,62 para 13,85 por cento. E também é possível verificar que o beta de todas as posições é igual quando o risco é minimizado.

Risco e Retorno

Até então foi discutido medidas para se calcular o risco em portfólios. O Próximo passo é considerar o retorno esperado de um portfólio, assim como o risco.

É definido \(E_{p}\) como o retorno esperado do portfólio. Isso é a combinação linear dos retornos esperados de cada componente da posição. E para simplificar os cálculos, podemos tomar como base que todos os retornos dos ativos serão considerados como a taxa livre de risco.

\[ E_p \sum_i^Nw_iE_ie\]

Pode-se definir que a melhor combinação de portfólios é aquela que minimiza o risco, mediante diferentes níveis de retornos esperados. Isso é definido com a fronteira eficiente, que é representada na linha sólida do gráfico.

Supondo que o objetivo principal é de maximizar o retorno esperado em relação ao risco, pode-se, usar a medida de risco ajustada, Sharpe Ratio:

\[ SR_p=E_p\div \sigma_p\]

A pergunta que pode ser feita é: “Como mudamos da posição atual para o portfólio ótimo?”

Nós agora queremos, para chegar no portfólio ótimo, o ratio em que todos os retornos esperados dos marginais VaRs devem ser iguais. Isso pode ser demonstrado através da fórmula abaixo:

\[ E_{i}/∆VaR_{i}=E_{i}/β_{i}=constante\]

A tabela abaixo mostra nossa posição em duas moedas, para cada assumimos um \(E{1}\) = 8 por cento e um \(E_{2}\) = 5 por cento. A posição original tem um Sharpe Ratio de 0.448, e o ratio do dólar canadense é de 0.1301. Isso implica que a posição em dólar canadense deve ser aumentada para melhorar a performance do portfólio.

Na melhor posição, o peso do dólar canadense foi de 66,67 para 90,21 por cento. A Sharpe Ratio do portfólio foi aumentada substancialmente de 0.448 para 0.551. E é possível verificar que as ratios são idênticas para os dois ativos no modelo otimizado.

Exemplo em Prática

Considere um portfólio com duas moedas estrangeiras, o dólar canadense (CAD) e o euro (EUR). Assuma também que essas duas moedas não são correlacionadas e apresentam uma volatilidade contra o dólar de 5% e 12%. Esse portfólio tem investido 2 milhões em dólares canadenses e 1 milhão em euro.

Realizando os cálculos para encontrar o VaR individual, e não diversificado, encontramos:

\[ [VAR_1 \ VAR_2 ]= [1.65 \ x \ 0.05 \ x \ 2 milhões\quad 1.65 \ x \ 0.12 \ x \ 1 milhão] = [165,000 \quad 198,000]\]

Esses números somados, nos garantem um VaR não diversificado de $363,000, o que é maior que o VaR do portfólio diversificado de 257,738, graças aos efeitos da diversificação.

Nós agora queremos adicionar uma posição aumentando em US$10,000 em dólar canadense. Primeiro, nós iremos calcular o método do VaR marginal.

\[ ∆VAR= α \ cov(R,R_P))\divσ_P =1.65 \ [$0.0050 \quad 0.00144]\div$0.156= [0.0528 \quad 0.1521]\]

Assim, nós acrescentamos a posição inicial com $10,000, o incremental VaR é:

\[ (∆VAR)`α= [0.0528 \quad 0.1521][$10,000 \quad 0 ]=0.0528 \ x $10,000+0.1521 \ x \ 0=$528\]

E ainda podemos comparar esse valor de incremental VaR obtendo a partir da reavaliação total da carteira. Adicionando $0.01 milhão na posição inicial, encontramos:

\[ \sigma_{p+a}^2W_{p+a}^2= [$2.01 \quad $1][0.05^2 \quad 0 \quad 0 \quad 0.12^2 ][$2.01 \quad $1]\]

O que nos dá um \(VAR_{p+a}\) = $258,267. Em relação ao \(VAR_{p}\) inicial de $257,738, o exato incremento foi de $529. Note o quão perto o cálculo do incremental VaR usando o marginal se aproximou do cálculo com a reavaliação total. Essa aproximação linear acabou sendo excelente por conta da mudança de posição ser bem pequena.

Continuando com essas duas posições, podemos calcular o componente VaR do portfólio usando \(CVAR_{i}=\triangle VAR_{i}x_{i}\) que é:

\[ [CVAR_1 \quad CVAR_2]=[0.0528 \ x \ $2 milhões \quad 0.1521 \ x \ 1 milhão]= [$105,630 \quad $152,108]=VAR[0.41 \quad 0.59]\]

Se verifica que estes dois componentes somados juntos dão o total valor de VaR de $257,738. O maior componente é o euro, que apresenta a maior volatilidade. Podemos calcular a mudança no VaR se a posição do euro for zerada. Como o portfólio apresenta somente dois ativos, o novo VaR sem a posição em euro é simplesmente o VaR individual da posição em dólar canadense, . O VaR incremental da posição em euro é de ($257,738 – $165,000) = $92,738.

Conclusões

Durante este artigo foi mostrado como se manejar risco utilizando de medidas analíticas conhecidas como VaR Tools.

A partir delas, vimos que o VaR é muito mais do que simplesmente uma medida de um ativo, e pode promover maneiras de gerenciamento de risco através das ferramentas mostradas.

No final, risco é apenas um dos componentes do processo de gerenciamento de portfólios. Também deve-se atentar aos retornos esperados e que o papel do gerente de portfólio é conseguir encontrar a melhor combinação entre esses dois componentes, risco e retorno.

Referências:

JORION, Philippe. Portfolio Risk: Analytical Methods. In: JORION, Philippe. Value At Risk: The New Benchmark for Managing Financial Risk. 3. ed. New York: Mcgraw Hill Companies, 2007. p. 159-185.

Posted by Vinícius Custódio in Derivativos & Riscos, 0 comments