Entendendo A Teoria Moderna do Portfólio
Desenvolvida nos anos 50, a teoria moderna do portfólio (TMP) de Harry Markowitz revolucionou a ciência da gestão de portfólio, rendendo a ele um prêmio Nobel de economia pelo seu trabalho com o artigo “Portfolio Selection” (1952), e livro “Portfolio Selection: Efficient Diversification” (1959).
A teoria do portfólio apresenta um modelo de montagem de carteira que analisa os ativos com suposições de risco, retorno e correlação futuros. A partir dos dados é calculado uma série de possíveis alocações, entre essas possíveis alocações os portfólios que maximizam o retorno esperado e minimizam o risco formam a chamada fronteira eficiente. A TMP leva em consideração que o investidor sempre deseja ter o maior retorno possível dado determinado nível de tolerância ao risco.
Uma das características do modelo é que ele tende a colocar carteiras mais diversificadas na fronteira eficiente. Os benefícios da diversificação já eram conhecidos muito antes da criação da TMP, mas não era algo a que os investidores davam tanta importância, era mais comum focar em tentar achar ativos singulares que dariam os maiores retornos com menor volatilidade. A TMP fez com que os efeitos da diversificação ficassem ainda mais claros, demonstrando os ganhos de eficiência com medidas quantitativas, grande parte do motivo dessa estratégia ganhar tanta popularidade pode ser atribuída ao trabalho de Markowitz.
Construção da Fronteira Eficiente
As informações necessárias para calcular a fronteira eficiente são apenas o retorno esperado dos ativos a serem considerados para compor a carteira, a volatilidade de cada um e a covariância entre eles.
Não há uma maneira certa de obter as estimativas de retorno, essa é a parte mais subjetiva do modelo, assumir que os retornos futuros tendem a seguir a média dos retornos passados é um modo comum de estimativa, outra opção comum que provavelmente é mais precisa seria utilizar a estimativa de um especialista na área. Para estimar a volatilidade costuma-se usar o desvio padrão como medida ilustrativa, no entanto, o artigo utilizará a variância para o cálculo de medida de volatilidade com o intuito de simplificar o entendimento das operações, tanto a variância quanto a covariância entre os ativos podem ser extraídos da série histórica de retornos.
A variância mede o grau de dispersão dos retornos em relação à média, ela é calculada subtraindo cada retorno pela média, elevando ao quadrado os resultados e então dividindo a soma dos quadrados pelo número de retornos calculados subtraídos por um.
$$\sigma ^{2}=\frac{\sum_{t=1}^{T}(R{t}-\widetilde{R})^{2}}{T-1}\ $$
Onde:
\(\sigma ^{2}\) representa a variância
\(R{t}\) representa o retorno t
\(\widetilde{R}\) representa a média dos retornos
\(T\) representa o número total de retornos usados no cálculo
A covariância mostra a relação da direção do movimento entre dois ativos diferentes, caso os ativos demonstrem uma tendência a se mover em conjunto o resultado do cálculo seria positivo e caso a tendência seja eles se moverem em direções opostas a covariância seria então negativa. Para calcular a covariância basta fazer o somatório do produto das diferenças dos retornos em relação à média de ambos os ativos e dividir o resultado pelo número de retornos analisados subtraído por um.
$$\sigma_{a,b}=\frac{\sum_{t=1}^{T}(R_{A_{t}}-\widetilde{R_{A}})(R_{B_{t}}-\widetilde{R_{B}})}{T-1}$$
Onde:
\(\sigma_{a,b}\) representa a covariância entre A e B
\(R_{A_{t}}\) representa o retorno t da variável A
\(R_{B_{t}}\) representa o retorno t da variável B
\(\widetilde{R_{A}}\) representa a média dos retornos de A
\(\widetilde{R_{B}}\) representa a média dos retornos de B
\(T\) representa o número de retornos usados no cálculo
Usando as estimativas de retorno e os resultados de variância e covariância é possível calcular o retorno esperado e volatilidade dos portfólios. Os retornos são calculados com a multiplicação peso de cada ativo pelo seu respectivo retorno esperado e então somando os resultados.
$$R_{p}=\sum_{i=1}^{}W_{i}R_{i}$$
Onde:
\(R_{p}\) representa o retorno esperado do portfólio
\(W_{i}\) representa a porcentagem do valor da carteira destinada ao ativo i
\(R_{i}\) representa o retorno esperado do ativo i
A variância do portfólio é um pouco mais complicada de calcular, nela é preciso levar em consideração que o retorno dos ativos tem um certo grau de correlação, apenas multiplicar o peso dos ativo pelas suas volatilidades, assim como é feito com o retorno, traria um resultado maior que o real, pois não seria levado em conta o poder de diminuição do risco que a diversificação oferece. Para fazer o cálculo da variância primeiro é feito com a multiplicação do vetor de pesos pela matriz de covariância, obtendo assim um vetor, e então outra multiplicação do vetor de pesos transposto pelo vetor resultante. A fórmula abaixo funciona para um número infinito de ativos pois utiliza matrizes para o cálculo, diferente de uma fórmula como \(w_{1}^{2}\sigma_{1}^{2}+2w_{1}w_{2}\sigma_{1,2}+w_{2}^{2}\sigma_{2}^{2}\) que funciona apenas em carteiras com dois componentes.

Onde:
\(\sigma_{p}^{2}\) representa a variância do portfólio
\(W_{1}\) representa a porcentagem do valor da carteira destinada ao ativo i \(\sigma_{i}^{2}\) representa a variância do ativo i
\(\sigma_{i,j}\) representa a covariância entre os ativos i e j
Com as fórmulas e informações prontas, basta utilizar um software para otimizar os pesos dos ativos, de forma que seja obtido a carteira menor variância para determinado retorno. Esse processo deve ser repetido em diversos pontos de retorno até que se forme uma boa aproximação da curva da fronteira eficiente.
Exemplo prático
Neste exemplo será usado o Excel para fazer os cálculos e a função solver será utilizada para encontrar os pontos eficientes. Serão considerados 4 ativos, IBRx50, IRF-M, IFIX e dólar, com séries históricas de retornos mensais desde agosto de 2017 a junho de 2020.
IBX50 – Índice que reflete o rendimento da bolsa brasileira, semelhante ao ibovespa, ele é composto pelas 50 empresas mais negociadas na B3, o diferencial do IBRX50 para o Ibovespa é a adição do Market cap das ações disponíveis em free float no cálculo para ponderar a representatividade de cada ação. O mercado de ações é considerado por muitos o investimento que oferece a maior rentabilidade, a troco de uma alta volatilidade, essas características tornam ações um ativo atraente para ser integrado na montagem de portfólio, onde seu risco pode ser mitigado pela diversificação.
IRF-M – Índice de títulos públicos de renda fixa divulgado pela Anbima, representa a performance dos títulos públicos pré-fixados pela simulação de uma carteira teórica com títulos LTN (pré-fixados) e NTN-F (pré-fixados com pagamento de cupons) de todas as datas de vencimentos acima de 1 mês. Instrumentos de renda fixa são outra boa opção de investimento, com baixo risco e fraca correlação com ações, seus rendimentos mais estáveis se mostram valiosos em cenários de crise econômica.
IFIX – Índice de FIIs (fundos imobiliários) que contém quase todos os FIIs negociados na B3, utiliza o market cap para a ponderação. FIIs acompanham bem o desempenho do mercado imobiliário em geral e são um ótimo hedge contra a inflação.
Dólar – A moeda americana por si só não é uma alternativa tão comum de investimento, o que a torna uma boa candidata a integrar a carteira é sua correlação negativa com ações brasileiras, sendo melhor até do que o ouro na sua função de hedgear a carteira.
A matriz de covariância pode ser obtida a partir da ferramenta de análise de dados, basta selecionar a opção de covariância e colocar no intervalo de entrada as séries de retornos, assim será a matriz será gerada, ela contém a variância dos ativos na diagonal principal e a covariância entre cada um deles. A partir da fórmula do cálculo da variância do portfólio e com o uso dessa matriz pode ser obtida a variância da carteira, multiplicando a coluna de pesos transposta pela matriz de covariância e multiplicando a linha resultante pela coluna de pesos.

O retorno do portfólio pode ser calculado com o uso da função “SOMARPRODUTO” que retorna a soma dos produtos de matrizes correspondentes, ao selecionar a coluna de pesos e a coluna de retornos esperados com essa função, o resultado obtido será o retorno esperado do portfólio.
Agora que a volatilidade e o retorno do portfólio estão prontos finalmente é hora de utilizar o Solver para encontrar as composições de menor variância. Na janela de parâmetros, o objetivo definido deve ser a célula da variância do portfólio e a opção de mínimo deve ser selecionada, a alteração de células variáveis deve ocorrer apenas na coluna de pesos e duas restrições devem ser adicionadas, a restrição fixa faz a soma dos pesos deve se igualar a 1 e a segunda restrição é o valor do retorno desejado. Ao término da computação os pesos resultantes representarão a carteira de menor volatilidade para o retorno dado. Então, ao repetir o processo diversas vezes com curtos intervalos de retorno se obtém o gráfico da fronteira eficiente.
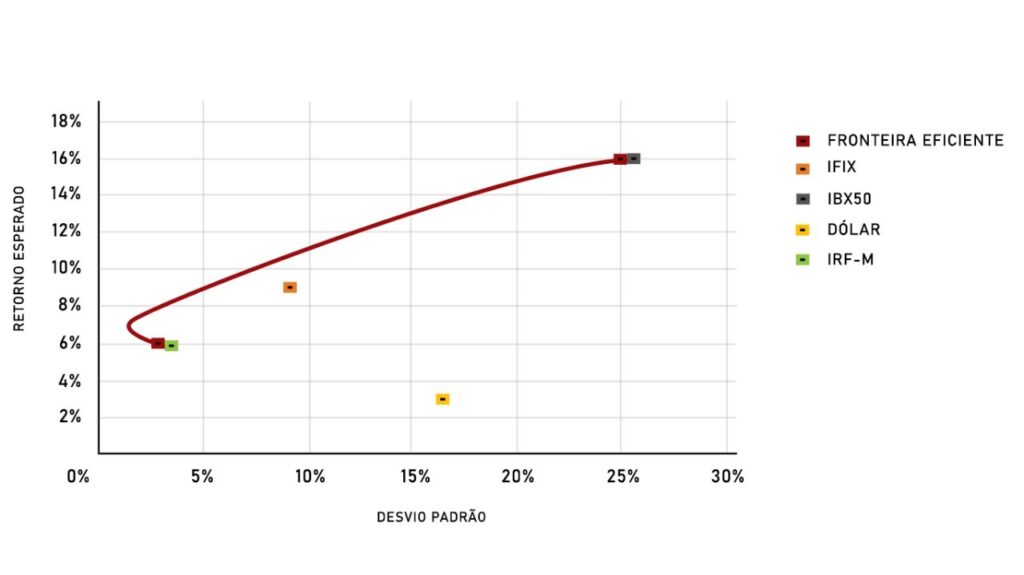
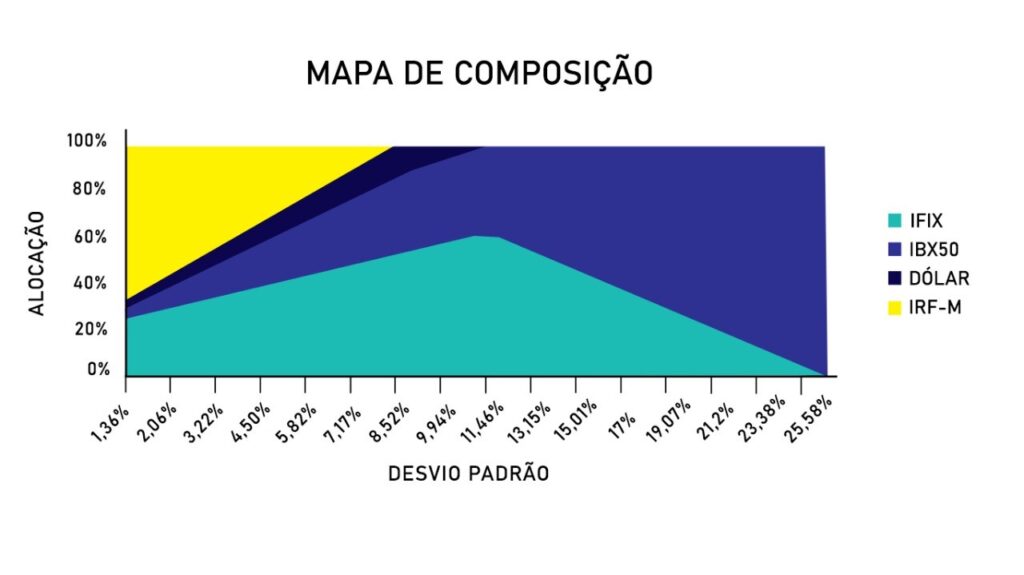
Utilizando os pesos obtidos pode ser feito um gráfico de área para ilustrar a composição da carteira em função do risco, esse gráfico é chamado de mapa de composição, nele é representado a porcentagem da alocação em cada ativo da carteira para as diferentes volatilidades da parte superior da fronteira eficiente.
Capital Market Line
A TMP implica que não existe uma combinação possível de ativos selecionados fora da fronteira eficiente que oferece maior retorno dado determinado nível de risco, no entanto, ao levar em consideração a possibilidade de tomar emprestado ou aplicar parte do dinheiro à taxa livre de risco, é possível obter uma linha de retornos acima da fronteira eficiente, essa linha é chamada de Capital Market Line (CML).
Para o cálculo da CML é utilizado o índice de Sharpe, ele é obtido ao dividir pelo desvio padrão do portfólio o resultado da subtração do retorno do portfólio pela taxa livre de risco. Esse índice ilustra a proporção do retorno superior oferecido pela carteira ajustado ao risco, um Sharpe maior significa que há um maior retorno adquirido para cada ponto de volatilidade adicionado.
A CML é formada ligando o ponto da taxa de retorno livre de risco ao ponto do portfólio de maior índice de Sharpe da fronteira eficiente. Qualquer ponto anterior ao ponto de tangência na CML seria uma posição com a carteira parcialmente exposta ao risco do portfólio eficiente e qualquer ponto posterior seria uma carteira completamente exposta ao portfólio com tomada de empréstimo para alavancagem, isso faz com que a linha toda possua o mesmo índice de Sharpe que o portfólio de tangência, assim, por consequência, todas as alocações representadas na linha tem uma relação de risco e retorno superior aos demais portfólios na fronteira eficiente.
O gráfico abaixo ilustra a CML tendo a Selic a 2,25% como taxa livre de risco, o portfólio de tangência ficou com uma composição de 68,2% em IRF-M, 24,9% em IFIX, 3,5% em IBX50 e 3,4% em Dólar.

A equação da Capital Market Line se dá por:
$$R_p=r_f+\frac{R_T-r_f}{\sigma_T}\sigma_p$$
Onde:
\(R_p\) = retorno da CML
\(r_f\) = taxa livre de risco
\(R_T\) = retorno do portfólio de tangência
\(\sigma_T\) = desvio padrão do portfólio de tangência
\(\sigma_p\) = desvio padrão da CML
Perceba que a equação da CML consiste em uma equação de primeiro grau, tendo a taxa livre de risco como coeficiente linear, o Índice de Sharpe como coeficiente angular e \sigma_p como variável.
Teoria do Portfólio Pós-Moderna
A teoria do portfólio pós-moderna é uma versão da TMP que utiliza a semivariância como mensurador de risco. A semivariância difere da variância tradicional por levar em consideração apenas os retornos abaixo da média em seu cálculo, assim deixando de penalizar retornos positivos acima do esperado como risco. Há também o uso do índice de Sortino, feito para substituir o índice de Sharpe, que consiste em uma fórmula semelhante, com a única diferença sendo o uso da semivariância no denominador da fórmula.
A fronteira eficiente é uma importante ferramenta para a gestão de portfólio, podendo ser utilizada para auxiliar o balanceamento na alocação de ativos, nela ficam claros conceitos fundamentais da montagem de carteiras, como os princípios de diversificação e de risco e retorno.
Referências:
Markowitz, H. (1952). Portfolio Selection. The Journal of Finance, 7(1), 77. doi:10.2307/2975974
Araujo, Alcides & de Avila Montini, Alessandra. (2010). TEORIA DO PORTFÓLIO PÓS-MODERNA: UM ESTUDO SOBRE A SEMIVARIÂNCIA. 10.13140/2.1.2596.0645.
Gibson, R. C. (2013). Asset allocation: Balancing financial risk. New York: McGraw Hill Education.
Gruber, M. J., Brown, S. J., Goetzmann, W. N., & Sanvicente, A. Z. (2004). Moderna teoria de carteiras e análise de investimentos. São Paulo: Atlas.
