Month: March 2022

Mar

2022

Aplicação de ferramentas econométricas utilizando a linguagem R: Value-at-Risk (VaR), abordagem delta-Normal vs. abordagem GARCH

Introdução

O objetivo desse artigo é desenvolver uma linha de raciocínio da construção do processo de estimação de um Value-at-Risk a partir de uma volatilidade que varia com o tempo, por meio de uma modelagem ARMA-GARCH e comparar com resultados obtidos em um Value-at-Risk constante no tempo, utilizando dados do Mercado Financeiro Brasileiro, com foco na linguagem de programação R.

Estacionariedade

Primeiramente, devemos entender o conceito de estacionariedade, um dos pontos mais importantes ao estimar e fazer inferências em séries temporais. Para fins econométricos, trabalharemos com a estacionariedade fraca, onde temos que um processo estocástico (aleatório) será fracamente estacionário (ou estacionário de segunda ordem), caso sua (1) média e sua (2) variância forem constantes ao longo do tempo. Além disso, precisamos que a (3) covariância não dependa do tempo, mas sim apenas da ordem s de defasagem (distância temporal entre as observações). Sendo assim, precisamos satisfazer:

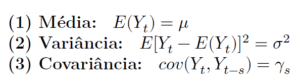
Mas por que é tão importante uma série temporal ser estacionária? Pois, caso tivermos uma série temporal não estacionária (média ou variância que variam com o tempo, ou ambas), não poderemos generalizar seu comportamento para outros períodos, somente para o período em consideração. Dessa maneira, caso nossa série for não estacionária, incorreremos no fenômeno de regressão espúria (sem sentido) e com isso não teremos valor prático.

Base de dados, linguagem R e bibliotecas

Utilizando-se da linguagem de programação R, com o propósito de efetuar o processo de modelagem, foi escolhida uma amostra de 01/01/2011 até 01/01/2021 da série diária de fechamento ajustada da pontuação do Ibovespa, obtida através do Yahoo Finance.

#carregando as bibliotecas necessárias
library(quantmod)
library(ggplot2)
library(scales)
library(forecast)
library(moments)
library(rugarch)
library(urca)

#inputs iniciais
ticker <- "^BVSP"
from <- "2011-01-01"
to <- "2021-01-01"

#puxando os dados do Yahoo Finance
price <- na.omit(Ad(getSymbols(ticker,
                               from = from,
                               to = to,
                               auto.assign = F)))

#calculando a diferenciação dos log-retornos
log_ret <- na.omit(diff(log(price)))
names(log_ret) <- "ibov"

Testes informais de estacionariedade

Como ponto de partida, recorremos para um teste informal, onde simplesmente analisamos o gráfico da nossa série temporal, nos dando assim uma pista acerca da sua provável natureza.

#plot da pontuação do Ibovespa
g1 <- ggplot() +
  geom_line(aes(y = price, x = index(price)),
            color = "darkblue", size = 0.5) +
  scale_x_date(date_labels = "%Y", date_breaks = "1 year") +
  scale_y_continuous(labels = number_format(big.mark = ".")) +
  labs(title = "Série diária do Ibovespa",
       x = "Data", 
       y = "Pontos", 
       caption = "Fonte: Yahoo Finance.", 
       color = "") +
  theme_light()

Gráfico 1

Observando o gráfico da pontuação diária do Ibovespa ao longo de dez anos, apesar de não podermos afirmar de antemão com exata certeza se a série é estacionária ou não, ela apresenta algumas características, como subidas e descidas bruscas, aparentando possuir uma tendência linear positiva e com isso evidenciando possível não-estacionariedade. Podemos também constatar a quebra de estrutura causada pela pandemia do Covid-19 a partir de março de 2020, porém essa análise em si foge do escopo desse artigo.

Consideraremos a hipótese de que os preços do mercado de ações seguem um passeio aleatório com tendência, em que cada termo Yt depende do termo anterior Yt-1 somado de um termo de erro, além de um coeficiente que escala a variável temporal t (tendência).

Dessa maneira, partiremos nossa análise mais detalhada a partir da diferenciação dos log-retornos dos preços (pontuação) de fechamento P no dia t em relação ao dia anterior t-1:

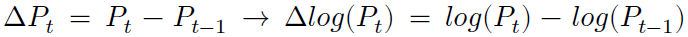
Tendo a série de retorno como:

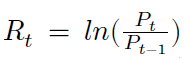
A transformação logarítma suaviza (lineariza) a série, enquanto a diferenciação ajudará a estabilizar a variância da série temporal. Para termos uma melhor visualização, criamos um gráfico dos dados dos log-retornos dos preços de fechamento ajustados do Ibovespa em que faremos nossos testes e teremos posteriores diagnósticos.

#plot da diferenciação dos log-retornos
g2 <- ggplot() +
  geom_line(aes(y = log_ret, x = index(log_ret)),
            color = "darkblue", size = 0.5) +
  scale_x_date(date_labels = "%Y", date_breaks = "1 year") +
  scale_y_continuous(labels = number_format(big.mark = ".")) +
  labs(title = "Série diária do Ibovespa",
       x = "Data", 
       y = "Log-retornos (%)", 
       caption = "Fonte: Yahoo Finance. Elaboração do Autor.") + 
  theme_light()

Gráfico 2

A análise do gráfico com a transformação da primeira diferença dos log-retornos nos permite observar um valor esperado estável em torno de zero, informando-nos de que a série evolui ao redor da média ao longo do período de dez anos em questão, além dos dados aparentarem apresentar uma menor variabilidade (em relação à série somente da pontuação). Antes de iniciar os testes formais de estacionariedade, precisamos elucidar alguns conceitos importantes.

Função de Autocorrelação (FAC), Função de Autocorrelação Parcial (FACP) e Correlograma

Podemos definir a correlação serial (autocorrelação) como a forma em que uma variável Y qualquer se relaciona com seu passado, isto é, até que ponto o passado dessa variável afeta ela no presente. Denotando Yt como a variável no tempo t, então temos que seu coeficiente de autocorrelação ρs na defasagem será igual a:

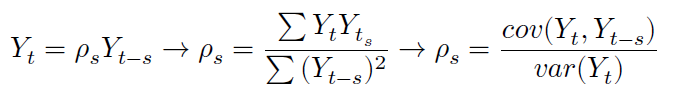
Onde o termo de erro 𝜇𝑡 é do tipo ruído branco (média zero, variância constante e i.i.d.) e −1 ≤ 𝜌 ≤ 1. O gráfico em que relaciona o 𝜌𝑠 com a defasagem 𝑠 é chamado de Correlograma.

Já o conceito de autocorrelação parcial é análogo ao conceito dos coeficientes em regressão múltipla, onde o coeficiente de autocorrelação parcial 𝜌𝑠𝑠 mede a correlação entre as observações que estão separadas por 𝑠 períodos, controlando as correlações nas defasagens intermediárias (menores que 𝑠), removendo seus efeitos.

Teste de Raíz Unitária (Dickey-Fuller)

Consideremos o processo estocástico sem constante e sem tendência denotado como 𝑌𝑡 = 𝜌𝑌𝑡−1 + 𝜇𝑡, subtraindo Yt−1 de ambos os lados, temos Δ𝑌𝑡 = (𝜌 − 1)𝑌𝑡−1 + 𝜇𝑡 → Δ𝑌𝑡 = 𝛿𝑌𝑡−1 + 𝜇𝑡, em que 𝛿 = (𝜌 − 1) e Δ = operador da diferença. Nesse caso, testaremos as seguintes hipóteses:

Processos Autorregressivos – AR(p)

É uma extensão do modelo de passeio aleatório, podendo ser incluídos termos mais distantes no passado. Nesse caso, o modelo depende linearmente de termos passados, com coeficientes para cada termo – podemos dizer que é um modelo de regressão em que os termos anteriores são os próprios preditores. Em um modelo autorregressivo de ordem p, teremos:

Onde 𝜇𝑡 é ruído branco.

Esse modelo nos informa que o valor estimado de Yt (expressos em torno de seus valores médios) dependerá de seus valores em períodos anteriores (com proporção 𝛼𝑝) adicionados de um termo aleatório.

Processos de Médias Móveis – MA(q)

É uma combinação linear de termos passados de ruído branco. Matematicamente, em um modelo de médias móveis de ordem q, teremos:

Onde 𝜇𝑡 é ruído branco.

O processo de média móvel estará sempre associado aos erros do modelo. Além disso, os pesos poderão ser diferentes conforme a importância das observações passadas.

Processos Autorregressivos de Médias Móveis – ARMA(p, q)

É a combinação dos dois modelos, em que haverá termos autorregressivos p e termos de média móvel q. Em um processo autorregressivo de médias móveis de ordem (p, q), teremos:

Já se tivermos que diferenciar a série em d vezes para torná-la estacionária, teremos uma série integrada de ordem 𝑑 → 𝐼(𝑑), e então, teremos um processo autoregressivo integrado de médias móveis – ARIMA(p, d, q).

Critério de Informação de Akaike (AIC)

Quando usamos um modelo estatístico para representar o processo que gerou nossos dados, perdemos observações (informações). É aí que o AIC entra ao estimar a quantidade relativa de informação perdida dado certo modelo, logo quanto menos informação um modelo perde, maior é a qualidade desse modelo. Em outras palavras, ele compara diversos modelos, e nos informa aquele que possui melhor qualidade (menor AIC) em relação aos outros. Por definição, temos que o 𝐴𝐼𝐶 = 2𝑘 − 𝑙𝑛(𝐿*), em que:

𝑘 → número de parâmetros estimados

𝐿* → valor máximo da função de máxima verossimilhança

Um destaque importante é de que o AIC procura o melhor trade-off entre a qualidade de ajuste (avaliado pela verossimilhança) e penalizando modelos em que mais parâmetros são utilizados.

A metodologia Box-Jenkins

O objetivo do método elaborado pelos estatísticos George Box e Gwilym Jenkins é de aplicar modelos ARMA ou ARIMA para encontrar o modelo que melhor se ajuste aos dados passados em séries temporais. Precisamos que as observações sejam estacionárias, para que possamos interpretar e efetuar inferências, a partir de uma base válida. O método consiste em três principais etapas, sendo elas: (1) identificação do modelo, (2) estimação dos parâmetros do modelo escolhido, e (3) verificação do diagnóstico.

(1) Identificação do modelo: as principais ferramentas que utilizaremos serão a Função de Autocorrelação (FAC) para estipular a ordem máxima q possível de processos de média móvel, a Função de Autocorrelação Parcial (FACP) para estipular a ordem máxima p possível de processos autorregressivos e seus respectivos Correlogramas resultantes (representações das FAC e FACP contra a extensão da defasagem).

Primeiramente faremos o Teste de Raíz Unitária de Dickey-Fuller sobre nossa série dos log-retornos, para testarmos nossas hipóteses e assegurar que estamos trabalhando com uma série estacionária.

#teste de Dickey-Fuller para os log-retornos
ur.df(log_ret, type = "none", lags = 0) #ou utilizar o summary

##The value of the test statistic is: -54.4401

Considerando que como resultado temos o valor da estatística teste igual a −54, 4401 e para um nível de significância de 𝛼 = 5, 00%, temos −1, 95 como nosso valor crítico, podemos dizer que rejeitamos a hipótese nula de não estacionariedade, uma vez que o valor calculado é menor do que o valor crítico.

Agora que testamos e sabemos que estamos lidando com uma série estacionária, partimos para a visualização do Correlograma da Função de Autocorrelação (FAC), para estipularmos a ordem máxima q possível de processos de média móvel.

#plot da Função de Autocorrelação (FAC)
g3 <- ggAcf(x = log_ret, lag.max = 10) +
  labs(title = "Autocorrelograma dos log-retornos do Ibovespa",
       subtitle = "Intervalo de confiança de 95%",
       y = "Função de Autocorrelação (FAC)", 
       x = "Defasagens") + 
  theme_light()

Gráfico 3

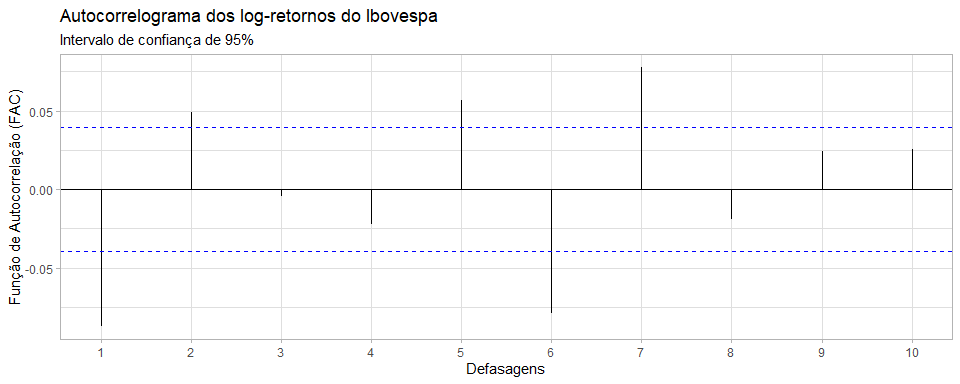
Podemos observar que possuímos aproximadamente até sete termos 𝜌𝑠 que ficam de fora do nosso intervalo de confiança de 95% (linha tracejada em azul) e por isso testaremos modelos com termos até MA(7).

Por outro lado, devemos visualizar também o Correlograma da Função de Autocorrelação Parcial (FACP), para determinarmos a ordem máxima p dos nossos termos autorregressivos.

#plot da Função de Autocorrelação Parcial (FACP)
g4 <- ggPacf(x = log_ret, lag.max = 10) +
  labs(title = "Autocorrelograma dos log-retornos do Ibovespa",
       subtitle = "Intervalo de confiança de 95%",
       y = "Função de Autocorrelação Parcial (FACP)",
       x = "Defasagens") + 
  theme_light()

Gráfico 4

Como podemos observar, possuímos até cinco termos 𝜌𝑠𝑠 que ficam fora do nosso intervalo de confiança, logo testaremos até um AR(5). Dessa maneira, testaremos todas as combinações possíveis de modelos até um ARIMA(5, d, 7) e escolheremos o que melhor se ajusta aos nossos dados a partir do Critério de Informação de Akaike (AIC).

#encontrando o modelo que se melhor ajusta
best_fit <- auto.arima(log_ret,
                       max.p = 5,
                       max.q = 7,
                       ic = "aic",
                       approximation = F,
                       trace = T)

## ARIMA(2,0,2) with non-zero mean : -13372.71
## ARIMA(0,0,0) with non-zero mean : -13324.64
## ARIMA(1,0,0) with non-zero mean : -13343.37
## ARIMA(0,0,1) with non-zero mean : -13341.66
## ARIMA(0,0,0) with zero mean     : -13326.20
## ARIMA(1,0,2) with non-zero mean : -13343.73
## ARIMA(2,0,1) with non-zero mean : -13343.53
## ARIMA(3,0,2) with non-zero mean : Inf
## ARIMA(2,0,3) with non-zero mean : -13377.81
## ARIMA(1,0,3) with non-zero mean : -13341.82
## ARIMA(3,0,3) with non-zero mean : -13376.80
## ARIMA(2,0,4) with non-zero mean : -13376.17
## ARIMA(1,0,4) with non-zero mean : -13355.28
## ARIMA(3,0,4) with non-zero mean : -13374.79
## ARIMA(2,0,3) with zero mean     : -13379.29
## ARIMA(1,0,3) with zero mean     : -13343.34
## ARIMA(2,0,2) with zero mean     : -13381.08
## ARIMA(1,0,2) with zero mean     : -13345.25
## ARIMA(2,0,1) with zero mean     : -13345.05
## ARIMA(3,0,2) with zero mean     : Inf
## ARIMA(1,0,1) with zero mean     : -13345.64
## ARIMA(3,0,1) with zero mean     : Inf
## ARIMA(3,0,3) with zero mean     : -13378.30

## Best model: ARIMA(2,0,2) with zero mean

A partir do processo iterativo de checar o melhor modelo entre vários, podemos observar que o modelo com menor perda de informação (menor AIC), portanto o de melhor qualidade é o autorregressivo de médias móveis – ARMA(2,2) sem constante. Partimos então para a segunda etapa da Metodologia de Box-Jenkins.

(2) Estimação dos parâmetros do modelo escolhido: para estimar os coeficientes dos parâmetros, recorreremos para a estimativa por máxima verossimilhança. Considerando que o modelo de maior qualidade é do tipo ARMA(2,2) sem constante, temos a seguinte equação para nossa série de retornos:

Onde 𝜀𝑡 é ruído branco.

#obtendo os coeficientes estimados do modelo
arima_fitted <- fitted(best_fit)
best_fit$coef

##  ar1         ar2          ma1        ma2
## -1.6441653   -0.8185129   1.5642812  0.7268909

A partir dos coeficientes estimados, podemos descrever o processo como sendo um modelo do tipo:

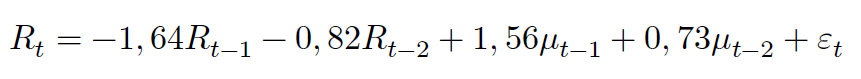
Podemos observar que nossos retornos no tempo t, ceteris paribus, são negativamente influenciados pelos retornos em t-1 e t-2 com grandeza -1,64 e -0,82, respectivamente, e positivamente influenciados por termos aleatórios em t-1 e t-2 com grandeza 1,56 e 0,73, respectivamente.

De forma a visualizar a comparação entre o modelo que estimamos e os valores realizados, elaborou-se um gráfico.

#plot dos log-retornos reais vs. estimados pelo modelo
g5 <- ggplot() +
  geom_line(data = log_ret, 
            aes(x = index(log_ret), 
                y = ibov, 
                color = ""), size = 0.5) +
  geom_line(data = arima_fitted, 
            aes(x = index(log_ret), 
                y = arima_fitted,
                color = " "), size = 0.5) + 
  scale_x_date(date_labels = "%Y", date_breaks = "1 year") +
  scale_y_continuous(labels = number_format(big.mark = ".")) +
  scale_color_manual(labels = c("Realizados", "Estimados"), 
                     values = c("darkblue", "gold")) + 
  labs(title = "Log-retornos reais vs. estimados",
       subtitle = "Série diária do Ibovespa",
       x = "Data", 
       y = "Log-retornos (%)", 
       color = "") +
  theme_light() + theme(legend.title = element_blank(), 
                        legend.position = "bottom")

Gráfico 5

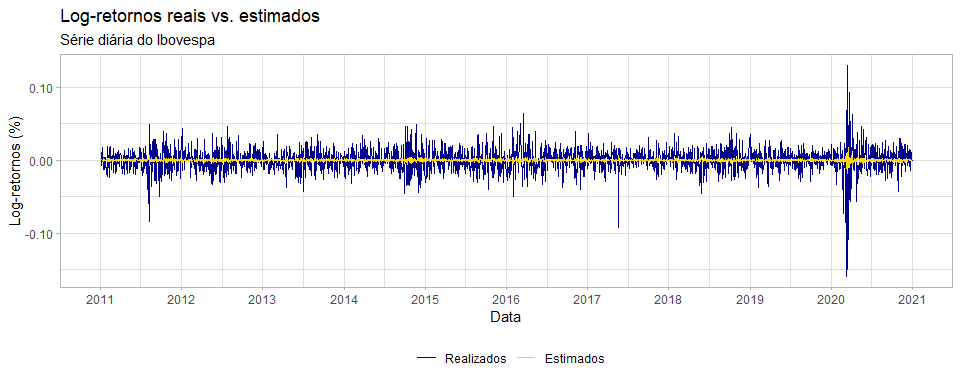
Por meio de uma análise gráfica, podemos observar que os valores dos parâmetros que estimamos parecem estar ajustados aos nossos dados. Apesar disso, precisaremos efetuar outros testes para obter essa confirmação, partindo assim para a terceira etapa.

(3) Verificação do diagnóstico: iremos checar se os resíduos (termos de erro) da equação que estimamos são do tipo ruído branco. Caso tivermos o resultado de que nossos resíduos não são completamente aleatórios, nosso modelo estimado não foi capaz de explicar completamente o comportamento determinístico da nossa série, portanto não seria um bom modelo.

Para fazermos testes formais em relação aos resíduos, podemos usar novamente a Função de Autocorrelação (FAC) e o Teste de Raíz Unitária de Dickey-Fuller.

#resíduos do modelo estimado
resid <- best_fit$residuals

#FAC dos resíduos do modelo estimado
g6 <- ggAcf(resid, lag.max = 15) +
  labs(title = "Autocorrelograma dos resíduos do modelo estimado",
       subtitle = "Intervalo de confiança de 95%",
       y = "Função de Autocorrelação (FAC)", 
       x = "Defasagens") + 
  theme_light()

Gráfico 6

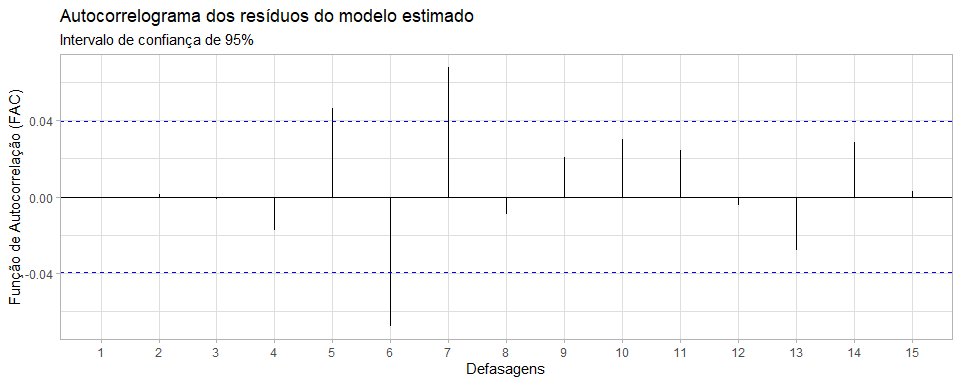
Como os coeficientes de autocorrelação 𝜌𝑠 estão dentro do nosso intervalo de confiança de 95%, podemos dizer que nosso modelo está bem especificado. Fazendo o teste de Dickey-Fuller, podemos observar em valores estatísticos.

#teste de Dickey-Fuller para os os resíduos do modelo estimado
ur.df(resid, type = "none", lags = 0) #ou utilizar o summary

## The value of the test statistic is: -49.3669

Considerando que o resultado que temos para o valor da estatística teste é igual a −49, 3669 e para um nível de significância de 𝛼 = 5, 00%, temos −1, 95 como nosso valor crítico, podemos dizer que rejeitamos a hipótese nula e portanto nossos resíduos não possuem correlação serial, sendo assim, conseguimos explicar a parte determinística da nossa série de dados temporais com sucesso – de fato nossos resíduos são valores aleatórios do tipo ruído branco.

Momentos de uma série: assimetria e curtose

Um fato estilizado que temos em séries temporais de ativos financeiros é a da distribuição de caudas gordas, em que expõe que há a baixa probabilidade de eventos raros ocorrerem, sendo aqueles que se situam nas caudas de uma distribuição Normal (risco de cauda).

Como os investidores comumente estão mais preocupados com perdas inesperadas do que com ganhos inesperados, as discussões tendem a ser voltadas para a cauda esquerda (perdas). Temos essas condições, pois as decisões tomadas no mercado financeiro dependem de comportamentos humanos (imprevisíveis), em que há evidências de que a distribuição dos retornos ao invés de serem normais, apresentam características de Assimetria (Skewness) e Curtose.

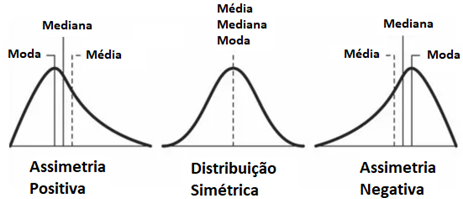
A Assimetria (relacionada ao terceiro momento de uma série) é uma medida referente à falta de simetria em determinada distribuição de probabilidade. Considerando que a distribuição Normal possui assimetria zero, conseguimos um indicativo de quanto a distribuição desvia-se da Normal. Em uma Distribuição Simétrica (Normal), a média é praticamente igual à mediana. Em uma Assimetria Negativa (left-skewed), a mediana é maior que a média e em uma Assimetria Positiva (right-skewed), a média é maior que a mediana. A Figura 1 descreve muito bem visualmente os três casos citados.

Figura 1

Já a Curtose (relacionada ao quarto momento de uma série) aborda o achatamento (forma) da curva de distribuição de probabilidade. Uma distribuição com alta Curtose possui um pico mais definido e caudas longas mais gordas, enquanto uma distribuição com baixa Curtose possui um pico mais arredondado e caudas finas menores.

Figura 2

Se a Curtose = 3, temos uma função Mesocúrtica (Normal). Se a Curtose > 3, temos uma função Leptocúrtica (de caudas longas). Já se a Curtose < 3, temos a função Platicúrtica (mais achatada que a Normal), conforme a Figura 2 ilustra.

#histograma dos log-retornos
g7 <- ggplot(log_ret, aes(x = log_ret)) + 
  geom_histogram(aes(y =..density..), colour = "black", fill = "darkblue") +
  geom_density(alpha = 0.35, fill = "gold") +
  scale_x_continuous(labels = number_format(big.mark = ".")) +
  labs(title = "Histograma dos log-retornos",
       subtitle = "Série diária do Ibovespa",
       x = "Log-retornos (%)", 
       y = "Frequência") +
  theme_light()

Gráfico 7

Ao nos depararmos com o histograma dos log-retornos, podemos observar em maior detalhe o comportamento da distribuição da nossa série, percebendo que eles seguem uma distribuição muito parecida com a distribuição Normal, porém contendo uma quantidade maior de observações na parte esquerda da cauda.

#momentos da série e estatísticas descritivas
skewness(log_ret) #assimetria negativa: moda > mediana > media

## ibov
## -0.9043515

kurtosis(log_ret) #leptocurtica (mais alongada)

## ibov
## 15.46513

summary(log_ret)[c(1, 3, 4, 6), 2]

## Min.: -0.1599303  Median: 0.0002812
## Mean: 0.0002161   Max.: 0.1302228

Como vimos anteriormente, a média da nossa série dos log-retornos é por volta de zero (0,0002161), com uma alta amplitude, tendo valores compreendidos de aproximadamente −15, 99% até 13, 02%. A partir do valor de −0, 90 do coeficiente de Skewness, podemos observar também que nossa série possui uma assimetria negativa, evidenciando que a curva de distribuição possui uma cauda mais alongada na esquerda (conforme o histograma nos mostra).

Além disso, pelo fato do coeficiente de Curtose ser maior que 3 (com o valor de 15,46), temos que a distribuição é do tipo leptocúrtica, isto é, menos achatada do que a curva de distribuição Normal.

Aglomeração de Volatilidade e o Modelo de Heterocedasticidade Condicional Autoregressiva Generalizada (GARCH)

Outro fato estilizado conhecido que temos em séries de ativos financeiros é o do fenômeno característico de aglomeração por volatilidade (onde há períodos em que a volatilidade exibe grandes oscilações, seguidos por períodos relativamente mais estáveis). Em termos gerais, temos que, grandes oscilações tendem a ser seguidas por grandes oscilações e pequenas oscilações tendem a ser seguidas por pequenas oscilações.

Trabalhar com a volatilidade (desvio-padrão dos retornos) dos preços das ações é de interesse dos investidores, uma vez que podemos sugerir que alta volatilidade pode significar grandes lucros/prejuízos, portanto maior incerteza. Além disso, em mercados voláteis, aumenta-se a dificuldade em captar recursos por partes das empresas nos mercados de capitais.

Considerando que estamos utilizando a primeira diferença dos log-retornos do Ibovespa, observamos conforme o Gráfico 2, que nossa série frequentemente exibe grandes oscilações (a mais recente sendo na crise do Covid-19 em março de 2020), sugerindo que a variância da série temporal financeira muda ao longo do tempo (heterocedasticidade). Podemos modelar essa variância variante, abordando primeiro o modelo de Heterocedasticidade Condicional Autorregressiva (ARCH), depois generalizando-o, chegando no modelo GARCH.

Denotemos nossos resíduos 𝜀𝑡 como seguindo um processo estocástico de ruído branco 𝜇𝑡 (média zero, variância constante e i.i.d.) escalado por um desvio-padrão que depende do tempo 𝜎𝑡, temos então 𝜀𝑡 = 𝜎𝑡𝜇𝑡. Como modelaremos o processo da variância como um processo autorregressivo, temos que a variância de hoje é composta pela variância de períodos anteriores ponderada por um coeficiente 𝛼𝑝:

Como não conseguimos propriamente observar a , Engle demonstrou que podemos utilizar a regressão dos resíduos ao quadrado no tempo t em relação aos resíduos ao quadrado dos períodos anteriores como proxy (aproximação) da variância:

Sendo um termo quadrático, quando houver grandes variações nos preços dos ativos financeiros, seu valor será alto e quando for relativamente pequeno, é por causa de variações pequenas.

Generalizando o modelo ARCH(p), chegamos ao modelo GARCH(p, q), onde a variância condicional de 𝜇𝑡 depende não somente dos resíduos quadráticos em períodos anteriores, mas também de sua variância condicional de períodos anteriores. Temos então p termos defasados dos resíduos quadráticos e q termos das variâncias condicionais defasadas:

Note que é determinístico, uma vez que depende de valores passados e já conhecidos. Sendo assim, temos que os modelos do tipo GARCH(p,q) não são estocásticos, apesar de ser.

#elevando os resíduos ao quadrado
resid_quad <- resid^2

#FAC dos resíduos ao quadrado
g8 <- ggAcf(resid_quad, lag.max = 15) +
  labs(title = "Autocorrelograma dos resíduos a quadrado",
       subtitle = "Intervalo de confiança de 95%",
       y = "Função de Autocorrelação (FAC)", 
       x = "Defasagens") + 
  theme_light()

Gráfico 8

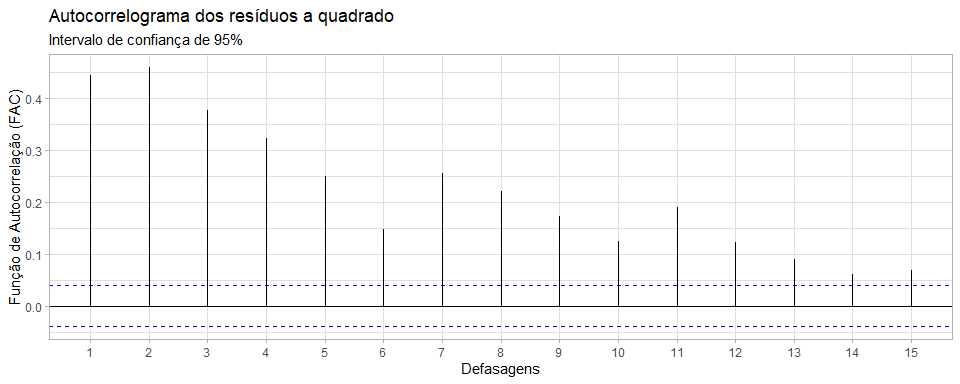
A partir da FAC e a FACP dos resíduos quadráticos do nosso modelo estimado, podemos verificar se os termos de ruído branco são dependentes e podem ser previstos. Caso os resíduos forem do tipo ruído branco estrito, serão independentes de média zero e normalmente distribuídos. Dessa forma, os coeficientes de autocorrelação no Correlograma da FAC e FACP dos resíduos quadráticos estarão dentro dos intervalos de confiança de 95% tracejados em azul.

#FACP dos resíduos ao quadrado
g9 <- ggPacf(resid_quad, lag.max = 15) +
  labs(title = "Autocorrelograma dos resíduos a quadrado",
       subtitle = "Intervalo de confiança de 95%",
       y = "Função de Autocorrelação Parcial (FACP)", 
       x = "Defasagens") + 
  theme_light()

Gráfico 9

O que observamos na realidade, é que na FAC, os coeficientes de autocorrelação vão decaindo lentamente a cada nível de defasagem, enquanto que na FACP temos uma maior estabilização dos coeficientes de autocorrelação parcial a partir da sétima defasagem. Portanto, os resíduos quadráticos nos dão indícios de serem correlacionados, e com isso temos evidência de efeitos GARCH(p,q) que podem ser modelados.

Primeiro, precisaremos especificar nosso modelo, em que de forma a simplificar nosso estudo, usaremos um GARCH(1,1) em conjunto com o ARMA(2,2) que estimamos. Além disso, de forma a captar melhor os efeitos de Assimetria e Curtose vistos anteriormente, utilizaremos a distribuição t-Student ao invés da Normal.

#especificando o modelo
t_garch_spec <- ugarchspec(
  variance.model = list(model = "sGARCH", garchOrder = c(1,1)),
  mean.model = list(armaOrder = c(2,2), include.mean = T),
  distribution.model = "std"
  )

Após especificarmos nosso modelo, estimamos os valores ajustados para nossa série de variância e podemos observar parte dela em conjunto com a série dos log-retornos e dos erros do modelo.

#encontrando os valores estimados do modelo ARMA(2,2)-GARCH(1,1)
fit_t_garch <- ugarchfit(spec = t_garch_spec,
                         data = log_ret)

#salvando os valores estimados
fitted_t_garch_series <- cbind(log_ret, 
                               fit_t_garch@fit$sigma,
                               fit_t_garch@fit$z)
names(fitted_t_garch_series) <- c("logret", "sigma", "et")

#dez primeiros valores 
head(fitted_t_garch_series, 10)

##              logret        sigma         et
## 2011-01-04   0.0050755741  0.01626328    0.279099381
## 2011-01-05   0.0109329350  0.01626328    0.639257936
## 2011-01-06  -0.0072280967  0.01587222   -0.458175560
## 2011-01-07  -0.0074234534  0.01538869   -0.517944765
## 2011-01-10   0.0009986875  0.01496752    0.003470236
## 2011-01-11   0.0042120304  0.01442680    0.245567330
## 2011-01-12   0.0170359473  0.01395652    1.186934784
## 2011-01-13  -0.0128133031  0.01418372   -0.902250006
## 2011-01-14   0.0030918908  0.01411208    0.187455965
## 2011-01-17  -0.0046768342  0.01365121   -0.410604085

#dez últimos valores
tail(fitted_t_garch_series, 10)

##              logret       sigma        et
## 2020-12-15   0.010133307  0.01267530   0.7428032
## 2020-12-16   0.015387351  0.01255479   1.2140346
## 2020-12-17   0.001778878  0.01284386   0.1424534
## 2020-12-18  -0.004053670  0.01246990  -0.3271978
## 2020-12-21  -0.014232466  0.01216374  -1.2268025
## 2020-12-22   0.002857587  0.01247546   0.1551960
## 2020-12-23   0.012886325  0.01213166   0.9820493
## 2020-12-28   0.010079948  0.01221818   0.8263367
## 2020-12-29   0.003555172  0.01218063   0.2806311
## 2020-12-30  -0.001415523  0.01188386  -0.1246335

Value-at-Risk (VaR): abordagem delta-Normal vs. abordagem GARCH

O Value-at-Risk é uma medida estatística de se medir o risco de perda em determinados ativos ou portfólios. De maneira geral, dado determinado nível de significância 𝛼 (ou um nível de confiança 1−𝛼) e um horizonte de tempo (dias, semanas, meses etc.), podemos dizer que a perda máxima não excederá a nossa estimação do VaR para o período em questão. O nível de confiança serve para determinar o grau de certeza em relação a medição (níveis de confiança mais elevados implicam em perdas mais elevadas), enquanto o horizonte temporal nos informa o intervalo que estamos avaliando (sendo que quanto maior for esse horizonte, maior tenderá a ser a perda estimada).

Para nosso estudo, compararemos: (i) a abordagem delta-Normal e (ii) a abordagem GARCH. A primeira delas considera que os retornos seguem uma distribuição Normal, constante ao longo do tempo, sendo definida por:

Em que 1−𝛼 é o nível de confiança estabelecido; 𝜇 é a média dos retornos; 𝜎 é o desvio-padrão dos retornos; e é a inversa da Função de Densidade de Probabilidade (FDP), que nos gerará o quantil correspondente da distribuição Normal.

Já a segunda abordagem, que é o nosso foco, considera que a volatilidade varia conforme o tempo passa (fenômeno da aglomeração por volatilidade), usando da variância condicional dada pelo modelo GARCH(1,1) que estimamos. Dessa maneira, temos:

Em que é o desvio-padrão condicional em t, considerando o último dado em t-1; e a é a inversa da Função de Densidade de Probabilidade (FDP), que nos gerará o quantil correspondente da distribuição t-Student.

É importante destacar que uma perda que exceda o limite estabelecido pelo VaR, dado determinado nível de significância, não é capturada, sendo assim não nos informando acerca da magnitude da perda, acarretando em uma “brecha” no VaR. Apesar dessa e outras falhas (maiores detalhes sobre VaR), é uma medida amplamente utilizada na quantificação de risco no mercado financeiro, devido – a não só – a sua facilidade de implementação em backtestings.

O backtesting é uma ferramenta que viabiliza a verificação da consistência e comparação entre as perdas realizadas e as perdas estimadas pelo modelo, nos informando como ele se comporta, por meio da utilização de dados históricos. Esse processo, nos ajuda a reduzir a sub-estimação do VaR, dando maior segurança para instituições que necessitem de capital para arcar com eventuais perdas. Além disso, também ajuda a reduzir a sobre-estimação, fazendo com que instituições não tenham que ser estritamente conservadoras, segurando mais capital que o necessário, possibilitando assim uma maior flexibilidade.

Primeiramente dividiremos nossa amostra em duas, onde utilizaremos as observações 1 até 1575 como teste e validaremos seu comportamento nas 895 observações restantes (1576 até 2470).

#observações teste e validação
set <- length(log_ret["2011-01-04/2017-05-17"])

test <- 1:set #observações 1:1575
validation <- (set+1):nrow(log_ret) #observações 1576:2470

Depois disso, faremos o backtesting com o modelo que havíamos especificado anteriormente, possibilitando a obtenção dos parâmetros da distribuição, necessários para a previsão de nossos valores hipotéticos. Iremos re-estimar o modelo a cada nova observação e utilizaremos um nível de significância de 𝛼 = 5, 00%.

#backtesting
roll_garch <- ugarchroll(
  spec = t_garch_spec, #modelo especificado
  data = log_ret,
  n.ahead = 1,
  forecast.length = 1, #a partir dos dados de validação
  n.start = set,
  refit.every = 1, #re-estimando o modelo a cada nova observação
  refit.window = "recursive",
  calculate.VaR = T,
  VaR.alpha = 0.05, #nível de significância de 5%
  keep.coef = T
  )

#forma da distribuição da série
shape <- fitdist(distribution = "std", x = log_ret)$pars[3]
t_dist_quantile <- qdist(distribution = "std", shape = shape , p = 0.05)

#valores previstos
validation_VaR <- mean(log_ret[validation]) +
  roll_garch@forecast$density$Sigma * t_dist_quantile

Com o backtesting feito, podemos elaborar um gráfico de forma a visualizar o Value-at-Risk com a abordagem GARCH em comparação com o Value-at-Risk com a abordagem delta-Normal.

#plot do VaR delta-Normal, VaR GARCH e retornos
g10 <- ggplot() +
  geom_line(aes(y = validation_VaR, 
                x = index(log_ret[validation]), 
                color = ""), size = 0.5) +
  geom_point(aes(y = log_ret[validation],
                 x = index(log_ret[validation]),
                 color = as.factor(log_ret[validation] < validation_VaR)), 
             size = 1.5) +
  geom_hline(aes(yintercept = sd(log_ret) * qnorm(0.05), color = " "),
             size = 0.5) +
  scale_y_continuous(labels = scales::number_format(accuracy = 0.01,
                                                    decimal.mark = '.'),
                     expand = expansion(c(-0.01, 0.01))) +
  scale_color_manual(labels = c("VaR GARCH", "VaR delta-Normal", "Retornos", 
                                "Retornos < VaR GARCH"),
                     values = c("darkcyan", "gold", "gray", 
                                "darkblue")) + 
  labs(title = "VaR GARCH(1,1) vs. VaR delta-Normal",
       y = "%", 
       x = element_blank(), 
       color = "") + 
       theme_light() + theme(legend.position = "bottom")

Gráfico 10

A partir de uma análise gráfica, podemos perceber que temos algumas observações (pontos em azul) que são menores que o VaR estimado pela abordagem GARCH (linha em verde ciano), porém que são maiores que aquelas estimadas pelo VaR delta-Normal (linha em amarelo). Além do gráfico, de forma a suportar nossa análise, podemos calcular o número de vezes cada um dos modelos excede em quantificar o risco.

#resumo de exceções
excecoes_dn <- sum(
  log_ret[validation] < 
    (mean(log_ret) + qnorm(0.05) * sd(log_ret[validation])))
excecoes_garch <- sum(log_ret[validation] < validation_VaR)
melhor_abordagem <- if(
  excecoes_dn < excecoes_garch){"ARMA-GARCH"} else{"delta-Normal"}

cat(" Número de excedências com a abordagem delta-Normal:", excecoes_dn,
    "\n",
     "Número de excedências com a abordagem ARMA-GARCH:", excecoes_garch,
    "\n",
     "A abordagem", melhor_abordagem,
    "consegue captar melhor os valores excedentes!")

## Número de excedências com a abordagem delta-Normal: 21
## Número de excedências com a abordagem ARMA-GARCH: 47
## A abordagem ARMA-GARCH consegue captar melhor os valores excedentes!

Dessa forma, temos que o VaR constante sobre-estima o risco, enquanto que o VaR com variância condicional aparenta se adequar melhor, possibilitando a captura de maiores retornos, sendo uma ferramenta de predição mais efetiva em nosso estudo.

#última etapa: previsão
garch_prev <- ugarchforecast(fit_t_garch, n.ahead = 3)

VaR_t1 <- round(
  (t_dist_quantile * garch_prev@forecast$sigmaFor[1]) * 100, 4)
VaR_t2 <- round(
  (t_dist_quantile * garch_prev@forecast$sigmaFor[2]) * 100, 4)
VaR_t3 <- round(
  (t_dist_quantile * garch_prev@forecast$sigmaFor[3]) * 100, 4)
VaR_dn <- round((sd(log_ret) * qnorm(0.05)* 100), 4)

cat(" VaR delta-Normal é: ", VaR_dn, "%.", "\n",
    "VaR-GARCH em t+1 é: ", VaR_t1, "%.", "\n",
    "VaR-GARCH em t+2 é: ", VaR_t2, "%.", "\n",
    "VaR-GARCH em t+3 é: ", VaR_t3, "%.")

## VaR delta-Normal é: -2.6804 %.
## VaR-GARCH em t+1 é: -1.7914 %.
## VaR-GARCH em t+2 é: -1.8108 %.
## VaR-GARCH em t+3 é: -1.8294 %.

Por fim, para concluirmos, estimamos os valores previstos em três dias a frente, nos dando uma ideia de quanto as instituições poderiam flexibilizar em sua tomada de risco em busca de maiores retornos no mercado financeiro em relação a uma medida fixa, mais rígida, que seria o VaR delta-Normal.

Referências

GUJARATI, D. N.; PORTER, D. C. “Econometria Básica”, 5. ed. Bookman: Porto Alegre, 2011.
BUENO, Rodrigo De Losso da Silveira. “Econometria de Séries Temporais”, 2. ed., 2012.
Engle, Robert. “GARCH 101: The Use of ARCH/GARCH Models in Applied Econometrics”. Journal of Economic Perspectives — Vol. 15, No. 4, pp. 157–168, 2001.
Christoph Hanck, Martin Arnold, Alexander Gerber, Martin Schmelzer. “Introduction to Econometrics with R”, 2020. https://www.econometrics-with-r.org/
Alexios Ghalanos (2020). rugarch: Univariate GARCH models. R package version 1.4-4. https://cran.r-project.org/web/packages/rugarch/vignettes/Introduction_to_the_rugarch_package.pdf
Angelidis, Timotheos and Benos, Alexandros and Degiannakis, Stavros. “The Use of GARCH Models in VaR Estimation”. Published in: Statistical Methodology — Vol. 2, No. 1, pp. 105-128, 2004.

Mar

2022

Carta de Conjuntura Macro – Fevereiro

O mês de fevereiro ficou marcado pelo início do conflito no Leste Europeu, com a invasão russa à Ucrânia, culminando numa piora do cenário macroeconômico global, com aumento das percepções de risco pelos agentes econômicos e uma maior volatilidade nos mercados.

Os impactos da guerra sobre a inflação devem ser a principal consequência econômica do conflito, fato que ocorre num cenário já de elevada pressão nos níveis de preço e de alta inércia inflacionária, tendo em vista os acentuados choques de oferta e descasamentos nas cadeias mundiais de insumo. Neste cenário, as projeções são de um aperto monetário mais intenso, com revisões baixistas para a atividade econômica, sobretudo na Europa. No Brasil, dados relativos à atividade econômica vieram acima do esperado, enquanto inflação continua persistente e com tendência altista.

Atividade Econômica – Resultados do 4T21 surpreendem positivamente, apesar do cenário incerto

O Produto Interno Bruto (PIB) para o 4º trimestre de 2021 avançou 0,5% na comparação com o trimestre anterior, acima das expectativas do mercado (0,1%), e 1,6% ante mesmo período em 2020.

No ano, o PIB avançou 4,6% em 2021, ante recuo de 3,9% em 2020, resultado próximo às expectativas do mercado no início do ano, de 4,5%. Com este resultado, o PIB quebra a sequência de dois trimestres consecutivos de recuo, retornando ao patamar positivo e deixando um carrego estatístico de 0,3% para 2022.

Pela Ótica da Produção, o destaque positivo se deu ao setor agropecuário, que registrou um crescimento de 5,8%, refletindo o bom desempenho de lavouras com peso relevante na produção agrícola, como a soja (11%), trigo (25,8%) e o arroz (5,2%).

Apesar da desaceleração, o setor de serviços ainda registrou alta de 0,5%, ante 1,2% registrado no período anterior, e segue refletindo os efeitos positivos do processo de normalização da mobilidade urbana, devido à redução das medidas restritivas. Os destaques positivos foram os Serviços de Informação e Comunicação, que obtiveram avanço de 3,4% no período.

Já o setor industrial apresentou o terceiro recuo consecutivo, de 1,2%. Com exceção do setor de Construção, que avançou 1,5%, todos os demais apresentaram queda na atividade. Em dados mais recentes, a produção industrial de janeiro apresentou queda de 2,4%, demonstrando que a indústria ainda segue sofrendo as consequências da alta dos custos com energia elétrica e dos graves problemas na cadeia mundial de insumos, intensificados com a recente piora no abastecimento de semicondutores, impactando consequentemente, a produção de bens duráveis.

Pela Ótica da Despesa, o destaque foi o consumo das famílias, apresentando alta de 0,7% no trimestre e acumulando alta de 3,6% no ano de 2021. O crescimento observado reflete a melhora dos indicadores de mercado de trabalho e os efeitos positivos gerados pelos programas de transferência de renda por parte do governo, apesar das vendas do comércio varejista e do faturamento do setor de serviços perderem fôlego no período. Os gastos do governo também contribuíram positivamente, com avanço de 0,8% no trimestre.

A Formação Bruta de Capital Físico avançou 0,4% no período, e 3,4% na comparação com o 4T20. Os destaques são atribuídos a demanda por máquinas e equipamentos, que apresentou alta de 3,7% no trimestre e de 23,6% no consolidado do ano – resultado influenciado pelo crescimento das importações -, e a construção civil, com crescimento de 0,7%. Além disso, a taxa de investimento em preços correntes cresceu 0,6 p.p. no quarto trimestre de 2021, quando comparado com o mesmo período do ano anterior, subindo de 18,4% para 19%. A taxa de poupança reduziu durante o mesmo período, de 12,1% para 11,3%, gerando uma poupança externa positiva.

Por fim, as exportações líquidas contribuíram de forma ligeiramente negativa para o resultado do PIB na comparação com o último trimestre de 2020, enquanto as exportações avançaram 3,3% no quarto trimestre, as importações tiveram alta de 3,7%.

No mercado de trabalho, a taxa de desemprego – medida pela PNAD – foi de 11,1% para o trimestre encerrado em dezembro, levemente abaixo das expectativas do mercado (11,2%). A redução no desemprego se deu devido ao crescimento dos empregos formais e informais. No entanto, a média real dos salários decresceu de forma mais intensa do que o crescimento de empregos, o que afeta o consumo das famílias e retrai a massa salarial real.

Adicionalmente, o indicador de confiança do consumidor, divulgado pela FGV, também obteve melhora durante o mês de fevereiro, subindo 3,8 pontos no mês, para 77,9, o maior nível desde agosto de 2021 (81,8). O destaque se deu pelo aumento da intenção de compras de bens duráveis, que estava em queda há cinco meses consecutivos.

Política Monetária – Redução do ritmo com previsão de ciclo mais longo

A inflação de fevereiro, medida pelo IPCA, apresentou alta mensal de 1,01%, acima do esperado pelo mercado (0,94%), uma aceleração relevante ante o mês de janeiro, onde o índice apresentou alta de 0,54%. A inflação acumulada em 12 meses fechou em alta de 10,54%.

Os destaques do índice se dão pela alta no segmento de Educação, que avançou 5,61% no mês devido aos reajustes anuais das mensalidades escolares, sendo responsável pelo avanço de 0,31 p.p. do índice. Ademais, Artigo de Residência (1,76%), Alimentos e Bebidas (1,28%) e Saúde e Cuidados Especiais (0,47%) também tiveram relevância sobre a alta.

Os combustíveis devem exercer pressão relevante sobre o índice em março, tendo em vista o reajuste no preço dos combustíveis nas distribuidoras promovido pela Petrobras, com elevação de 18,7% para a gasolina e 24,9% para o diesel.

Adicionalmente, outros fatores podem provocar novas revisões nas expectativas e no cenário inflacionário no curto prazo, como o cenário climático adverso e a manutenção dos preços das commodities em patamares elevados, impactados pelas preocupações com as possíveis restrições de oferta em torno da atual crise geopolítica. Em contraponto, a aprovação da PLP 11/20 deverá exercer um impacto baixista sobre o preço dos combustíveis e, consequentemente, sobre os níveis de preço.

Em linha com as expectativas do mercado, o Copom elevou a taxa Selic, em decisão unânime do comitê, em 100 pontos-base, para 11,75% a.a. na reunião de março. No comunicado que acompanhou a decisão, o Copom já adiantou que deve realizar uma alta de mesma magnitude na próxima reunião, com data para os dias 3 e 4 de maio. Na ata da primeira reunião de decisão de política monetária de 2022, no mês de fevereiro, o Copom demonstrou que está disposto a continuar o ciclo de aumento na taxa de juros, mas com ritmo mais lento. Entre os principais pontos citados, o comitê alertou sobre os riscos de incerteza da política fiscal e de preços de ativos e commodities, sendo os últimos amplificados com o recente conflito no leste europeu.

Complementarmente, o comitê registrou durante o mês que alguns indicadores mostraram evolução ligeiramente superior à esperada na virada do ano, com melhora no mercado de trabalho. No quadro atual, com a taxa de juros já em campo contracionista, a redução do ritmo em março permite o comitê discernir com maior precisão os reais efeitos do novo choque. Em síntese, os efeitos do conflito no Leste Europeu devem ser menos severos para os países da América Latina, mas o efeito adverso das commodities sobre os níveis de preço devem impactar a inflação doméstica, neste cenário, já partindo de um exercício de desinflação desafiador, é esperado um ciclo de aperto mais longo, como já precificado pelo mercado.

Política Fiscal e Cenário Político – Melhora do cenário fiscal com perspectiva de aumento da arrecadação para o ano

No cenário fiscal, a arrecadação pública deve seguir superior à média pré-pandemia, como ocorrera no ano passado, estimulada, dentre outros fatores, pela normalização dos programas de redução e diferimento de impostos lançados para o combate da pandemia, pelo impacto positivo da inflação na base de arrecadação e, sobretudo, pelo boom das commodities.

Em paralelo, a alta das commodities tem elevado a pressão por políticas de controle de preços, como a PLP 11/20, já sancionada. O cenário, no entanto, permanece positivo, com algumas projeções de mercado não descartando a possibilidade de novo superávit para o setor público em 2022. Segundo estimativas do Banco BTG Pactual, a arrecadação do governo central com commodities em 2022 deve atingir patamar próximo a R$ 270 bilhões.

Projeção: BTG Pactual. Valores em R$ bilhões.

No ambiente político, o mês de fevereiro foi marcado pela volta das atividades legislativas e pela intensificação das movimentações visando o ano eleitoral. O ambiente político vislumbrado em meados de 2021, de instabilidade e forte escalada da desarmonia entre os poderes, perdeu espaço, mediante a concentração de esforços para o processo eleitoral que, de forma mais acentuada, começa-se a estruturar.

O mês de fevereiro foi marcado pela discussão de possíveis medidas legislativas para conter a pressão inflacionária sobre o preço dos combustíveis. Após a tramitação de algumas propostas no legislativo, foi sancionado a PLP 11/20, que prevê a isenção de Pis/Cofins para o diesel, gás e querosene de aviação até o final de 2022, com um impacto estimado de R$ 16,1 bilhões (0,17% do PIB) para o governo federal. O projeto também modificou a regra de cálculo do ICMS sobre o diesel até o final de 2022, que passa a considerar a média do preço dos últimos 5 anos. O impacto estimado desta medida é de R$ 9,0 bilhões (0,09% do PIB) no ano para os Estados. A aprovação da medida, associada à melhora recente nos preços internacionais do petróleo, retirou da pauta a possibilidade de novas iniciativas por parte do Planalto para controle dos níveis de preço dos combustíveis a curto prazo.

Setor Externo – Apreciação do real com aumento da demanda por ativos brasileiros e guerra no Leste Europeu

O forte fluxo de dólares para o país, decorrente em grande parte, do crescimento da demanda global por ativos de países emergentes exportadores de commodities, fez com que a entrada líquida de dólares nos dois primeiros meses do ano atingisse o maior patamar desde 2012, com um ingresso líquido de divisas de US$ 9,0 bilhões no período.

Com a redução dos estímulos no mercado americano e a consequente saída de investimentos no mercado acionário, os investimentos estrangeiros em ações no Brasil atingiram patamares elevados, cerca de R$ 70 bilhões até o dia 7 de março, segundo a B3. Neste cenário, o dólar obteve queda de 2,71% no mês, sendo cotado a R$5,15 no fechamento e já acumulando uma queda próxima a 8% no ano, adicionalmente, o índice Ibovespa fechou o mês em 113.142 pontos, uma alta mensal de 0,89%.

No âmbito geopolítico, o mês de fevereiro foi marcado pelo início do conflito entre Rússia e Ucrânia, gerando impactos sobre a atividade econômica, tendo em vista as várias sanções impostas por diversos países membros da OTAN, como forma de retaliação à invasão russa.

A primeira rodada de sanções foi direcionada a bancos e patrimônios de oligarcas, mas, com a intensificação do conflito, medidas mais firmes foram impostas, como a retirada da Rússia do Swift – um sistema de transferências que fornece informações a bancos do mundo inteiro – e congelamento de reservas internacionais. Adicionalmente, diversas empresas privadas suspenderam suas operações em território russo.

O conflito, além de gerar perdas humanitárias, pressionou o preço de commodities da região. Produtos como o alumínio, gás natural, fertilizantes, milho, petróleo e trigo apresentaram alta volatilidade, e devem seguir apresentando tendências altistas no curto prazo. Neste cenário, é difícil mensurar os impactos causados pelo conflito na atividade doméstica, apesar da baixa participação da Rússia na corrente de comércio brasileira. Respondendo por apenas 0,7% das exportações do Brasil, e por 2,7% das importações no total acumulado dos últimos doze meses em fevereiro, a Rússia é a principal fornecedora de adubos e fertilizantes para o Brasil, com participação de cerca de 23% do total importado pelo país.

No cenário econômico, os destaques se dão por dados da atividade econômica, inflação, desemprego e política monetária na Europa e pelo desemprego e inflação nos EUA. Adicionalmente, na China, a implementação de novas medidas restritivas ganha força e resultados vêm acima das expectativas.

O desemprego para o mês de janeiro na Zona do Euro foi de 6,8%, abaixo do esperado pelo mercado (6,9%). O número representa uma queda ante dezembro (7,0%), com o afrouxamento de restrições melhorando a perspectiva no mercado de trabalho.

A inflação registrada para o período de janeiro de 2022 veio de acordo com as expectativas, representando um aumento de 0,3% ante dezembro e atingindo a máxima histórica do bloco, uma inflação anual de 5,1%. O ECB (European Central Bank) já havia optado por deixar a taxa de juros inalterada no início deste mês, no patamar de 0%, mas, devido à pressão inflacionária e os conflitos na Ucrânia, pode ser que o ECB siga o caminho do BoE (Bank of England) e adiante o hike sobre as taxas de juros.

Por fim, a atividade de manufatura da Zona do Euro em fevereiro subiu a 58,2, após ter registrado em janeiro o maior número dos últimos cinco meses. O alívio nos gargalos pelo lado da oferta resultou em melhores condições para a indústria, apesar de que a melhora não foi distribuída entre os membros do bloco e fábricas ainda enfrentam altas pressões inflacionárias.

Na China, na tentativa de conter o avanço de novos casos da variante Ômicron, o governo chinês decretou novo lockdown na cidade de Shenzhen e na província de Jilian, colocando 17,5 milhões de moradores em confinamento. Em paralelo, os dados da produção para os meses de janeiro e fevereiro vieram acima das projeções do mercado, com alta de 7,5% na comparação anual, contra alta esperada de 3,5%, conjuntamente, as vendas no varejo cresceram 6,7% durante o mesmo período, também acima dos 4,3% esperados pelo mercado.

Já nos EUA, o PMI de manufatura para o mês de fevereiro registrou 57,3, número levemente abaixo do esperado (57,5), e alta comparado aos 55,5 anteriores. O resultado vem de acordo com a redução das restrições impostas à cadeia de suprimentos, estimulando a atividade industrial no país.

Também surpreendendo, o número de criação de trabalhos nos EUA para o mês de fevereiro foi de 678 mil, muito acima do esperado (400 mil) por economistas. O resultado se deu pelo aumento de empregos nos segmentos de hospitalidade, educação e saúde. Além disso, a taxa de desemprego ficou em 3,8%, número inferior aos 3,9% projetados pelo mercado e menor número após o início da pandemia.

A inflação americana para o mês de fevereiro acelerou a 7,9% anualizados, de acordo com as expectativas do mercado. O número é o maior registrado nos últimos 40 anos, motivado pelas pressões inflacionárias causadas pelo preço de alimentos e commodities energéticas.

Por fim, pela primeira vez desde 2018, o Fed anunciou uma alta na taxa de juros americana, de 0,25 p.p., estabelecendo-a em 0,50% ao ano. A decisão não foi unânime, com um diretor optando por uma alta de 50 bps. O chairman do Fed, Jerome Powell, comentou logo em seguida que as próximas 7 reuniões do comitê terão altas, e que a taxa de juros americana deve terminar o ano em patamar entre 1,75% e 2%. Ainda, Powell citou o balanço do Fed, com perspectiva de começar a reduzi-lo já a partir da próxima reunião.

A decisão vem em linha com o esperado pelo mercado, que vê positivamente a medida tomada pelo Fed em momento de pressão inflacionária e robustez no mercado de trabalho americano.

Em síntese, o quadro para a atividade econômica permanece desafiador para os próximos meses, principalmente por conta das pressões inflacionárias, advindas dos descompassos entre oferta e demanda, aumento dos custos produtivos, e pelas recentes incertezas das consequências do conflito no Leste Europeu. O cenário é de maior cautela e de piora nas percepções de risco, com tentativas por parte do mercado de mensuração dos eventuais impactos causados pelo conflito sobre a atividade econômica. Por fim, as projeções são de piora do quadro inflacionário no curto prazo e tendência de maior contracionismo monetário por parte das principais autoridades monetárias, desestimulando ainda mais a atividade econômica.