Apesar de o modelo de precificação de ativos CAPM de Sharpe-Lintner ser o mais conhecido no mundo das finanças e adminstração, este não é o melhor modelo para se explicar os retornos de ativos que carregam risco. Uma das opções mais difundidas, e que iniciou o movimento chamado modelo de fatores para precificação, conhecido no mercado também por modelos multi-fatores ou smart beta é o modelo de 3 fatores de Fama e French1.
Neste modelo os retornos dos ativos é explicado não somente pelos retornos de mercado, o primeiro e principal fator, mas também por outros dois fatores conhecidos como SMB ( Small minus Big ) e HML ( High minus Low ), que referem-se respectivamente aos fatores de tamanho da firma e “valor” precificado, no qual a relação valor contábil sobre valor de mercado é a proxy. Uma ação com alta relação contábil sobre mercado é considerada uma empresa de “valor”, enquanto que no caso contrário se enquadram as chamadas empresas de “crescimento”, ou glamor.
As carteiras, que são construídas no final de junho de cada ano, são as interseções de duas carteiras formadas em tamanho ( Market Equity, ME ) e três carteiras formadas pela razão entre patrimônio líquido contábil e valor de mercado ( Book-to-Equity e Market Equity, BE/ME). O ponto de corte de tamanho para o ano t é o patrimônio mediano de mercado da Bolsa de Valore de Nova Iorque – NYSE, no final de junho do ano t. A métrica BE/ME para junho do ano t é o patrimônio contábil do último exercício encerrado em t-1 dividido por ME para dezembro de t-1. Os pontos de corte para BE/ME são os percentis 30% e 70% da NYSE. Desta forma são criados os seguintes seis portfólios:
| Firmas Pequenas | Firmas Grandes | |
|---|---|---|
| Ações Valor | Small Value | Big Value |
| Ações Neutras | Small Neutral | Big Neutral |
| Ações Crescimento | Small Growth | Big Growth |
Estes dois fatores extras são construídos a partir de seis carteiras do tipo long-short, determinadas pela interseção entre os dois critérios de classificação, tamanho e valor. Assim o fator SMB é calculado através da média dos retornos das empresas pequenas menos a média dos retornos das empresas grandes.
\(SMB = 1/3 (Small Value + Small Neutral + Small Growth)\ \qquad \qquad – 1/3 (Big Value + Big Neutral + Big Growth)\)
Da mesma forma, o fator HML é construído por uma carteira long-short montada com a média dos retornos das empresas de valor menos a média do retorno das empresas de crescimento.
\(HML = 1/2 (Small Value + Big Value) – 1/2 (Small Growth + Big Growth)\)
O fator de mercado é a carteira formada com todas as empresas listadas nas bolsas do país ponderadas pelo seu valor de mercado. O retorno do fator é, assim como no CAPM, o retorno em excesso ao ativo livre de risco. De posse dos retornos de nossos três fatores, o modelo de precificação de Fama e French segue a relação:
$$R_a = R_f + \beta (R_m – R_f) + \beta_s SMB + \beta_v HML$$
onde o retorno em excesso do ativo de interesse, \(R_a – R_f\) é explicado pelo familiar \(\beta\) de mercado, como no CAPM, mas também pelos recém introduzidos fatores SMB e HML, com exposições \(\beta_s\) e \(\beta_v\) respectivamente.
Por exemplo, se nosso ativo de interesse for uma ação de “valor” espera-se que a exposição ao fator HML seja alta, ou seja, \(\beta_v\) será um valor relativamente elevado (quando em comparação com ações de crescimento). Com esta maior exposição ao fator valor, esta ação capturará melhor os retornos proporcionados por HML que não estão incluídos no mercado. Fama e French (1993)2 argumentam que seu modelo explica muito melhor a seção cruzada (cross section) dos retornos das ações que o modelo mais simples, CAPM. Enquanto que este explica aproximadamente 60 a 70% dos retornos das ações, seu modelo multi-fatores é capaz de explicar mais de 90% das variações ocorridas nos preços.
Este modelo foi um dos precursores dos modelos multi-fatores que hoje estão em voga no mercado. Atualmente estes modelos estão inseridos dentro de “estilos de investimento”, onde por exemplo, uma determinada carteira pode ser formada com exposição unitária ao fator de mercado mais um viés para ações de valor. Diz-se que esta carteira está inserida no estilo “valor” de investimento. Com esta alocação o retorno esperado da carteira será o retorno esperado do mercado, pois seu beta de mercado é unitário, mais a exposição desta carteira ao fator valor vezes o retorno esperado deste fator. Se o fator valor possuir retorno esperado positivo esta carteira pode se beneficiar e bater o mercado.
Mas os fatores SMB e HML de fato possuem valor esperado de retorno positivos? O professor Kenneth French mantém em seu site pessoal um grande banco de dados com os históricos destes fatores e vários outros. É uma biblioteca bastante rica em dados que vários pesquisadores utilizam e pode ser acessada de forma livre em: http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html. Abaixo apresentamos um gráfico de série temporal dos três fatores, mercado, tamanho e valor. Lembrando que os retornos dos fatores tamanho e valor já estão em excesso ao fator mercado, ou seja, uma carteira exposta a SMB é remunerada tanto pelo mercado quanto pelo fator em si.
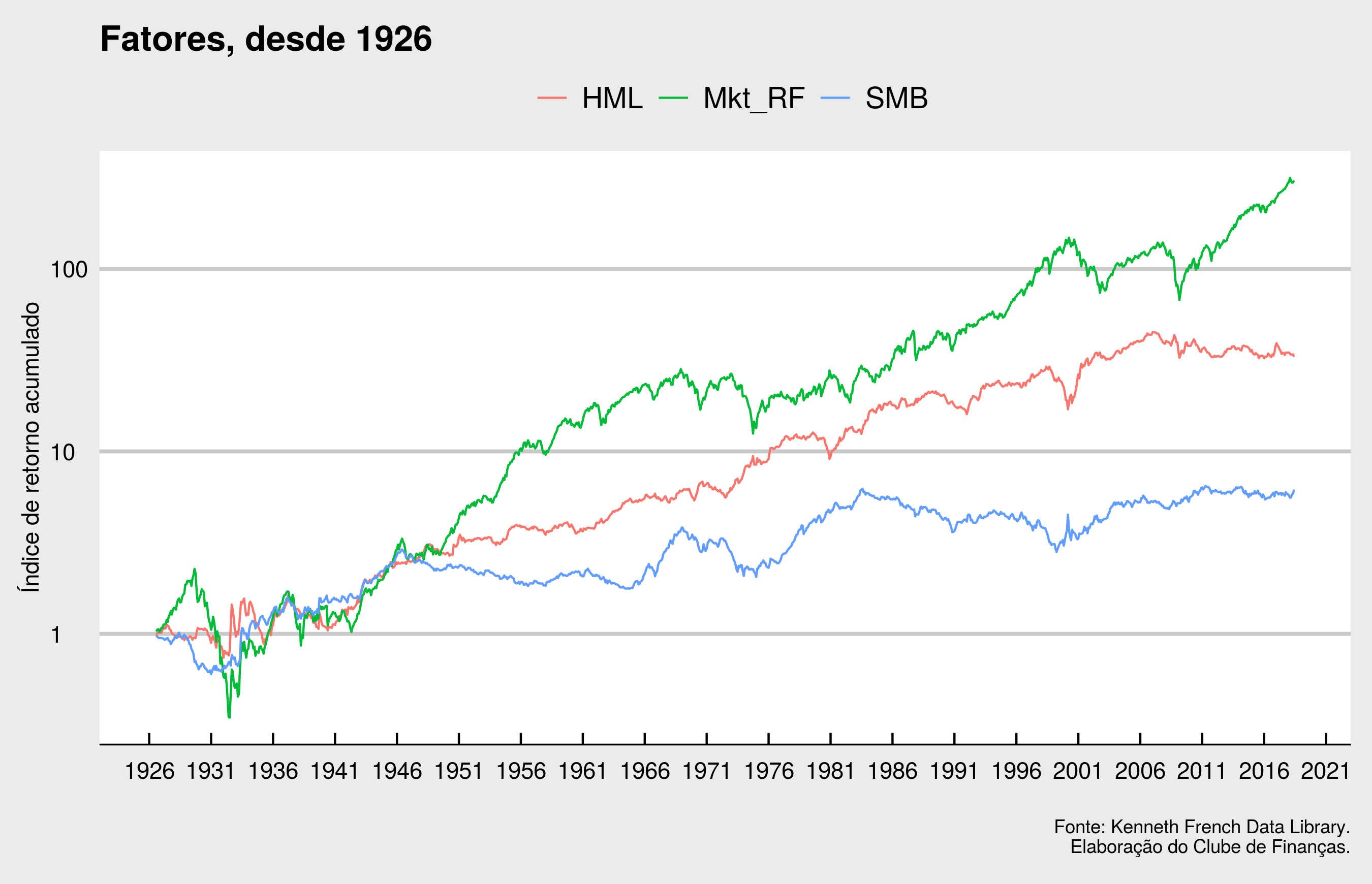
A cada dia novos fatores vêm sendo descobertos e alguns desbancados, sempre na busca de um modelo ideal de precificação que una parcimônia na quantidade de fatores explicativos, boa aderência aos dados empíricos e mais recentemente, com fundamentação em teoria econômica para explicar sua validade. Considerando que estes fatores podem ser isolados do retorno de mercado e investidos de forma individualizada e cumulativa, não é coincidência que hoje vivemos uma explosão de produtos “multi-fatores”, “com estilo”, “smart beta” e afins.
-
Fama, E. F., & French, K. R. (1992). The cross‐section of expected stock returns. the Journal of Finance, 47(2), 427-465. ↩
-
Fama, E. F., & French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of financial economics, 33(1), 3-56. ↩

