RAPMs – Risk Adjusted Performance Measures – Parte 1
Diversos artigos do núcleo de Risco & Derivativos abordam a questão de gerenciamento de risco em um portfólio ou instituição. Neles, os membros do Clube de Finanças dissertam sobre métricas como o VaR (Value at Risk), os avanços do ES (Expected Shortfall), Risco de mercado, Princípios de Basileia e Teoria do Valor Extremo. Essas métricas são relacionadas às exposições das instituições financeiras em determinados ativos ou conjunto de ativos (portfólio), normalmente sob responsabilidade de um gestor de risco de mercado. Entretanto, métricas de risco podem ser utilizadas por outros profissionais no mercado financeiro com propósitos diferentes, como o gestor profissional de ativos ou o investidor pessoa física.
No livro Quantitative Methods in Finance (2008), a Profa. Carol Alexander coloca diferentes papéis para o gestor de risco de mercado e o gestor de ativos. O primeiro possui a necessidade de mensurar o risco de um portfólio frequentemente (e.g. diariamente) e não possui como principal preocupação o retorno desse conjunto de ativos. Por outro lado, o gestor de ativos tem como prioridade gerar retorno para seus investidores, assim como reportá-los e contextualizar os riscos envolvidos. Em um fundo de investimentos, por exemplo, essas duas variáveis são observadas em relação ao benchmark.
Tomando um fundo de investimentos como referência, caso um gestor considere somente o retorno de um ativo ou portfólio, uma parte excessiva do patrimônio seria alocada em ativos com retornos esperados (E(r)) acima da média, porém, possivelmente com riscos proporcionais. Sob outra perspectiva, caso o gestor considere somente o risco, pouco do patrimônio do fundo seria alocado neste(s) ativo(s).
O intuito do presente artigo é introduzir algumas métricas de risco utilizadas na gestão de ativos, mais precisamente indicadores de risco e retorno, conhecidos como Risk Adjusted Performance Measures (RAPMs).
Os primeiros RAPMs foram introduzidos no mercado financeiro durante a década de 60, juntamente com o Capital Asset Pricing Model (CAPM), originalmente proposto por William T. Sharpe (1964) e posteriormente por John Litner (1965). Visto que muitos RAPMs estão ligados ao CAPM, começaremos o artigo com uma revisão desse modelo, já citado em outras publicações do Clube de Finanças.
O CAPM foi criado com base no trabalho de Harry Markowitz sobre diversificação e teoria moderna de portfólios, introduzida na década de 50. Apesar do tempo, esses trabalhos ainda são amplamente utilizados para estimativas de custo de capital e para avaliações da performance de gestão de portfólios, esse último, objeto deste artigo.
De forma breve, o modelo de escolha de portfólio desenvolvido por Markowitz (1959) presume que um investidor no tempo t-1 escolhe um portfólio que produz um retorno estocástico no tempo t. Como premissa, esse investidor é avesso ao risco e preocupa-se somente com a média e variância do retorno nesse período (entre t-1 e t). Nessa escolha, o investidor opta por um portfólio “média-variância-eficiente”, portanto, portfólios que i) minimizam a variância do retorno e ii) maximizam o retorno esperado, dada a variância do retorno.
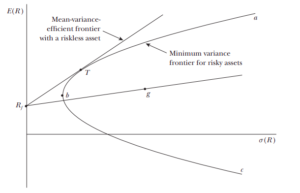
Fonte: Fama and French (2004)
A figura acima demonstra a intersecção entre o trabalho de Markowitz e o desenvolvimento do CAPM.
O eixo horizontal do gráfico mostra o risco de determinado portfólio através do desvio padrão dos retornos e o eixo vertical demonstra o retorno esperado dos portfólios. Ao longo da curva abc, a qual é chamada de “fronteira de variância mínima” ou fronteira eficiente, é possível observar portfólios de ativos que minimizam a variância do retorno em diferentes níveis de retorno esperado, nesse primeiro momento com uma restrição em relação aos empréstimos com taxas livres de risco. No ponto T, por exemplo, o investidor que aceita volatilidade pode encontrar um portfólio com retorno esperado maior sem adicionar tanto risco (portfólios com maior desvio padrão). O ponto T pode ser interpretado como um portfólio “média-variância-eficiente”.
Ao retirarmos a restrição de empréstimos com taxas livres de risco, a fronteira eficiente torna-se uma linha reta, como a que passa pelos pontos Rf e g. Para entendimento dessa curva, podemos imaginar um fundo que investe uma proporção x de seu patrimônio em um ativo livre de risco (títulos do tesouro dos Estados Unidos, T-bills, por exemplo) e 1-x em um portfólio g. Se todo o patrimônio for direcionado para ativos livre de risco, o retorno esperado será o ponto Rf (taxa de juros livre de risco) no eixo vertical. Dessa forma, combinações entre ativos livres de risco e alocações em g formam a linha Rf-g.
O portfólio g é uma dentre as infinitas combinações de ativos na curva abc e abaixo dela. Considerando a premissa de que o investidor opta por um portfólio ”média-variância-eficiente”, altera-se a inclinação da linha Rf-g até o ponto de tangência T, logo, nesse exemplo, os portfólios eficientes são combinações entre um ativo livre de risco e o portfólio T. Com um entendimento das distribuições dos retornos e a premissa de simetria de informações, os investidores tendem a optar pelo mesmo portfólio T, o qual os autores passam a denominar de M, em alusão ao “mercado”.
A reta Rf-M é definida como a Capital Market Line (CML), a representação gráfica de diversos portfólios que otimizam combinações de risco e retorno, tanto em cenários de investimento (lend), como captação (borrow) à taxas de juros livres de risco.
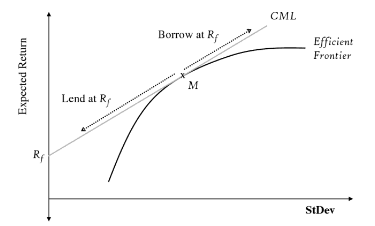
Fonte: Alexander (2008)
Feitas as considerações acima, podemos entrar no conceito do CAPM e entender a sua relação com outras métricas que serão apresentadas. O modelo surge como uma forma de explicar o retorno dos ativos como um agregado de componentes do retorno. Tradicionalmente ele é utilizado em um contexto onde um ativo com risco, como por exemplo a ação de uma empresa, está prestes a ser adicionado à um portfólio diversificado e busca responder a seguinte questão: qual deveria ser o retorno adicional para justificar a inclusão deste ativo no portfólio diversificado?
Após a introdução do conceito podemos passar para a sua definição. Originalmente, o modelo CAPM Sharpe-Lintner foi baseado no conceito de equilíbrio de mercado, onde o excesso de retorno esperado de um ativo i (E(Ri) – Rf) seria proporcional ao retorno adicional do mercado (E(Rm)-Rf), aqui citado como o portfólio M.
Equação 1:
![]()
Com base na fórmula acima e uma pequena manipulação algébrica, o retorno esperado de um ativo i é a taxa livre de risco Rf, mais um prêmio pelo risco, o qual é definido pelo Beta do ativo i (beta i) multiplicado pelo prêmio por unidade de “risco beta”, E(Rm) – Rf.
Na equação apresentada, o Beta do ativo i é a covariância dos retornos do ativo i e do mercado divididos pela variância do retorno do mercado. Na prática, ele pode ser calculado através de uma regressão linear simples dos retornos do ativo contra os retornos do mercado. O beta será o coeficiente angular da reta de regressão.
Equação 2:

Ao pensar em um modelo de regressão para estimar o retorno esperado de um ativo, podemos chegar na seguinte equação:
Equação 3:
![]()
Onde os componentes da equação continuam com o mesmo significado, porém, o retorno de determinado ativo não é explicado totalmente pelo excesso de retorno do mercado, surge um termo de erro aleatório ẽ.
Para facilitar o entendimento das métricas que serão apresentadas, faremos uma alteração no CAPM Sharpe-Lintner. Como já foi comentado, as equações 1 e 3 podem ser eficientes para responder a principal questão do CAPM e por consequência estimar o risco sistemático de um ativo individual ou um de um portfólio não gerenciado ativamente. Porém, ao aplicar essa fórmula para um portfólio gerido ativamente, o gestor pode selecionar ativos com um ẽ significativamente maior do que zero, em função de habilidades ou conhecimentos que não estão disseminados no mercado. Com isso, o portfólio não será explicado somente pelo seu beta, o que é plausível em um contexto onde existe um gestor de ativos, portanto, um ponto falho do CAPM Sharpe-Lintner.
Em estudos posteriores, autores como Jensen (1968), Douglas (1968), Black, Jensen & Scholes (1972), Fama & MacBeth (1973) e Fama & French (1992), encontraram que o intercepto da equação do CAPM é consistentemente maior do que a taxa livre de risco Rf. Além disso, as regressões mostraram que, em média, o prêmio por unidade de “risco beta”, é consistentemente menor do que o excesso de retorno do mercado em relação à taxa livre de risco, E(Rm) – Rf. Dessa forma, para facilitar o entendimento dos próximos tópicos do artigo, adotaremos a equação proposta por Jensen em seu trabalho de análise de performance de fundos mútuos.
Equação 4:
![]()
Onde o intercepto 𝛼 (alpha) pode ser entendido, segundo Jensen, como o retorno médio incremental no portfólio devido à habilidade do gestor de ativos. De outra forma, é possível definir o 𝛼, posteriormente denominado de alpha de Jensen, como o retorno do portfólio não explicado diretamente pelo retorno adicional do mercado em relação ao ativo livre de risco, E(Rm) – Rf.
RAPMs baseados no CAPM
Nessa parte do artigo apresentaremos os RAPMs que surgiram concomitantemente com o CAPM, logo, fazem referência ao modelo. Esses RAPMs introdutórios podem ser utilizados para rankeamento de portfólios por uma ordem de preferência, de acordo com as intenções do investidor ou gestor de ativos.
Sharpe Ratio
O Sharpe Ratio foi desenvolvido por WIlliam F. Sharpe e assim como os outros RAPMs leva em conta o retorno de um ativo em relação ao risco. O indicador é interpretado como o excesso de retorno de um ativo em relação ao ativo livre de risco, por unidade de volatilidade (𝜎 desvio padrão).

Aqui, fazemos a primeira referência à parte introdutória do artigo. O Sharpe Ratio é a inclinação da Capital Market Line (CML), portanto, quanto o retorno esperado do ativo ou portfólio aumenta/diminui com mudanças na volatilidade (𝜎 desvio padrão). De forma breve, portfólios com Sharpe ratios maiores tendem a ser priorizados por investidores e gestores de ativos em um rankeamento. É importante pontuar que, ao considerar o E(R) do ativo, presume-se que os retornos sejam normalmente distribuídos, o que muitas vezes não acontece na prática.

Fonte: Alexander (2008)
Treynor Ratio
Supondo a existência de um 𝛼 (vide equação 3) nos retornos de um ativo/portfólio com risco, sob a ótica do CAPM, Treynor propôs um indicador associado à esse retorno não correlacionado com o mercado.

O Treynor Ratio possibilita ordenar portfólios de acordo com os retornos não explicados pelos retornos de mercado, por unidades de risco sistemático (Beta).
Information Ratio ou Appraisal Ratio
O appraisal ratio possui suas origens na teoria proposta por RIchard Grinold e aprofundada por Clarke, de Silva e Thorley sobre a Law of Active Management, a qual busca conceituar o valor adicionado pelos gestores de ativos/portfólios. O appraisal ratio foi criado com o objetivo de mensurar e distinguir as habilidades dos gestores de ativos.
![]()
Como é possível observar na fórmula acima, gestores de portfólios com retornos ativos (𝛼) por unidade de risco (𝜎 desvio padrão), possuem um appraisal ratio maior.
Limitações
O CAPM tem sido utilizado de forma ampla desde a década de 60 até os dias atuais e diversas adaptações foram feitas ao modelo, como é possível observar na equação 4 e nos estudos de Jensen (1968), Douglas (1968), Black, Jensen & Scholes (1972), Fama & MacBeth (1973) e Fama & French (1992) citados anteriormente. Mesmo com a utilização frequente do CAPM, faz-se necessário entender as suas limitações e rigidez nas premissas.
O CAPM Sharpe-Lintner define que o prêmio de risco esperado por um ativo está relacionado somente com o seu risco sistemático, ou seja, a sua relação com o retorno adicional de um portfólio de mercado (E(Rm) – Rf). Conforme comentado anteriormente, em outros estudos foi possível rejeitar estatisticamente que o prêmio por unidade de “risco beta”, é consistentemente menor do que o excesso de retorno do mercado em relação à taxa livre de risco, E(Rm) – Rf, assim como o intercepto é maior do que o retorno de um ativo livre de risco Rf. Uma alternativa ao modelo CAPM Sharpe-Lintner já foi discutida anteriormente em um artigo do Clube de Finanças. Ao considerar outras variáveis além do retorno do mercado, o modelo de 3 fatores de Fama e French surge como uma alternativa para a precificação de ativos.
Quanto às premissas, o modelo pressupõe que: (1) todos os investidores possuem utilidades de maximização de riqueza, em um período, avessas ao risco e podem escolher diferentes portfólios somente em função de suas médias e variâncias, (2) não existem impostos e custos de transação, (3) todos os investidores têm visões homogêneas sobre os parâmetros da distribuição conjunta de probabilidade dos retornos dos ativos/portfólios e (4) os investidores podem emprestar e tomar emprestado a uma taxa livre de risco. Dessa maneira, podemos perceber que existe certa rigidez nas premissas e na formatação do modelo ao considerar, por exemplo, que o retorno adicional de um ativo é explicado somente pelo retorno do mercado ou que todos os investidores possuem visões homogêneas sobre o comportamento da distribuição de retorno de um ativo.
Parte 2
Na parte dois falaremos sobre o Kappa, Omega e Sortino Ratios, assim como traremos algumas aplicações práticas desses índices.
> Referências
Jensen, Michael C., The Performance of Mutual Funds in the Period 1945-1964. Journal of Finance, Vol. 23, No. 2, pp. 389-416, 1967.
Vidyamurthy, Ganapathy. Pairs trading : quantitative methods and analysis. Hoboken, N.J.: J. Wiley, 2004.
Jensen, Michael C. and Black, Fischer and Scholes, Myron S., The Capital Asset Pricing Model: Some Empirical Tests. Praeger Publishers Inc., 1972.
Alexander, Carol. “Market Risk Analysis, Quantitative methods in finance”. John Wiley & Sons, 2008.
Leibowitz, Martin L. Modern portfolio management: active long/short 130/30 equity strategies, 2009.
Sharpe, William F. Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk, The Journal of Finance, Vol. 19, No. 3, 1964.
Fama, Eugene F. and French, Kenneth R. The Capital Asset Pricing Model: Theory and Evidence, Journal of Economic Perspectives, Volume 18, Number 3, 2004.

