Introdução
Neste artigo será aplicado algumas técnicas de análise de risco em um portfólio de ações, com o intuito de obter uma análise mais práticas de tópicos estudados dentro do núcleo de Riscos & Derivativos do Clube de Finanças. O objetivo é aplicar diferentes técnicas de análise de risco e demonstrar como que os resultados obtidos podemos ser utilizados para o estudo do risco do portfólio.
As técnicas aplicadas serão: Value at Risk (VaR); Expected Shortfall; Stress Test; Matriz de correlação; Máximos Drawdowns, e o cálculo de alguns RAPMs.
O portfólio montado
O portfólio no qual iremos realizar as nossas aplicações, será uma carteira composto 100% por ações listadas na B3. Foram selecionadas as ações de algumas das maiores empresas da bolsa brasileira, visando englobar empresas sólidas e de diferentes setores de atuação, para evitar que riscos específicos de setores ou de empresas Small Caps distorçam os nossos cálculos.
Assim, o portfólio foi montado contendo 10 ações, todas com pesos igualmente distribuídos. São elas: ABEV3, B3SA3, BBDC3, BPAC3, ITUB3, MGLU3, PETR3, SANDB3, VALE3, WEGE3.
Value at Risk
O conceito de Value at Risk (VaR), foi introduzido pelo banco americano JPmorgan nos anos 90. Ele pode ser definido como a perda máxima que pode ocorrer com X% de confiança em um período de t dias.
Existem diferentes métodos possíveis para calcular VaR, diferentes métodos resultam em diferentes resultados. As duas formas mais comuns de se calcular, são através do método paramétrico e do método histórico, também conhecido como método não-paramétrico.
No método paramétrico, assumimos que os retornos seguem uma distribuição conhecida (normalmente a Gaussiana) e calculando o retorno esperado e o desvio padrão, podemos chegar no valor do VaR, para um dado nível de confiança.
Já o método histórico, como o próprio nome mostra, vai utilizar os retornos passados do portfólio para estimar a possível perda futura do mesmo.
De maneira geral, o cálculo da VaR envolve 4 etapas:
1. Determinar o horizonte de tempo em que é desejado estimar a perda potencial.
2. Selecionar o grau de confiança para o VaR que será estimado.
3. Criar uma distribuição probabilística dos possíveis retornos para o portfólio.
4. Calcular o VaR estimado.
Neste artigo serão aplicados o método paramétrico e o método não paramétrico no portfólio previamente montado. Ambos os métodos foram aplicados utilizando os níveis de confiança de 99%, 97,5%, 95%, que são tradicionalmente os níveis de confiança mais utilizados, e foi calculado o VaR do portfólio para 1 dia.

O que os resultados nos mostram é que por exemplo, a um nível de confiança de 95%, a perda máxima esperada do nosso portfólio para daqui 1 dia é de 2,96%.
Ressalte-se, porém, que se a perda registrada no período for superior ao VaR calculado, não significa que o cálculo do VaR está incorreto, apenas que o valor da queda está nos valores que excedem o nível de confiança utilizado. Quando se utiliza 95% de nível de confiança, isso significa que existe uma chance de 5% de o valor registrado superar o VaR calculado. Tal fato pode ser visualizado no gráfico abaixo:

Como sendo uma estatística quantitativa, o VaR captura somente riscos que podem ser quantificados, ou seja, ele não captura por exemplo, riscos de liquidez ou riscos operacionais.
Expected Shortfall
A Expected Shortfall, ou também conhecida como Conditional Value at Risk (CVaR), entra como uma espécie de complemento do VaR. Ela responde à pergunta de o que aconteceria se fosse registrado uma perda maior do que a perda máxima calculada pelo VaR. É visando esses casos que se calcula a Expected Shortfall.
A ideia do seu cálculo é selecionar todos os valores que estão fora do nível de confiança, e calcular uma média desses valores. De uma forma análoga, também pode-se definir o cálculo como sendo a área da distribuição que abrange os valores não contemplados pelo VaR
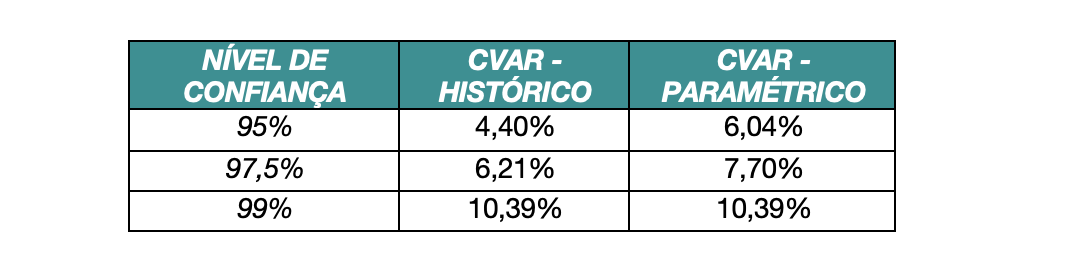
Vale destacar que o Extected Shortfall sempre dará um valor superior ao VaR, pois como foi visto pela sua definição, ele trata dos valores superiores ao Value at Risk.
A interpretação dos resultados funciona da mesma maneira que para o VaR. A perda média esperada para o período de 1 dia, caso ela ultrapasse o VaR, a um nível de confiança de 95%, é de 6,04% do valor inicial do portfólio.
Matriz de Correlação
Quando montamos o portfólio, foi destacado a importância de não selecionar muitas ações de empresas de um mesmo setor para evitar que eventos específicos de tais setores tenham uma influência muito grande sobre os cálculos. Em outras palavras, foram evitadas ações de empresas altamente correlacionadas, pois ações de um mesmo setor tendem a ter uma alta correlação.
A forma mais formal de analisar a correlação das ações de um portfolio de ações é através de uma Matriz de Correlação. Com ela podemos analisar como as diferentes ações do portfólio se correlacionam e avaliar de uma forma geral se a carteira está muito concentrada.

Analisando a Matriz de Correlação do portfólio, podemos ver que ele aparenta ser composto por ações não muito correlacionadas entre si. Como dito, ações de um mesmo setor tendem a ter uma correlação mais alta, podemos ver que as ações do Banco Bradesco (BBDC3) e do Itaú (ITUB3) possuem a maior correlação do portfólio. Por outro lado, a Suzano (SUZB3) e o Banco do Brasil (BBDC3) possuem a correlação mais baixa.
RAPM – Sharpe Ratio
Risk Adjustment Perfomance Measures (RAPM), são métricas de riscos utilizadas para compreender melhor a relação risco e retorno de investimentos. Eles foram criados nos anos 60, pelo William Sharpe, criador do Capital Asset Pricing Model (CAPM), e as duas ferramentas são muito interligadas.
O RAPM mais conhecido é o Sharpe Ratio, ele basicamente nos diz quanto que um investimento está retornando, comparado a uma taxa livre de risco. Ele pode ser calculado pela fórmula abaixo, onde Rp é o retorno do portfólio, Rf a taxa livre de risco e σp o desvio padrão do retorno do portfolio.
No gráfico abaixo, podemos ver o comportamento do índice de Sharpe do portfólio ao longo do tempo, onde a média foi de um pouco inferior a 2.

Máximo Drawdown
A principal utilidade do Máximo Drawdown é como uma métrica de risco, avaliando o desempenho passado do portfólio. Ele é usado pra nos mostrar as principais quedas passadas que o portfólio teve, em determinado período. No gráfico temos destacado os 5 maiores Drawdowns do portfólio nos últimos 3 anos.
Analisando o gráfico Underwater, podemos ter uma noção de como foram as principais quedas do portfólio nos últimos 3 anos.
Com essa ferramenta podemos observar como foram as quedas passadas do portfólio e, assim, ponderar se é um histórico de quedas que nos faria sentir seguros.

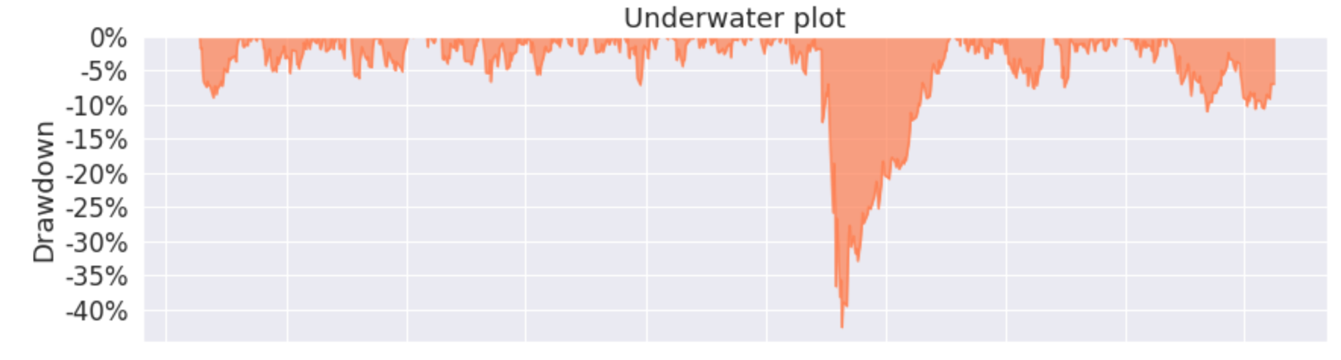
Analisando o gráfico Underwater, podemos ver que não foi um evento raro o portfólio registrar uma queda de aproximadamente 5%. Assim se um investidor não estiver disposto a se expor a uma volatilidade desse nível, o nosso portfólio não seria uma boa escolha de investimento.
Para exemplificar melhor a utilidade deste gráfico, vamos analisar o Underwater plot do Bitcoin.
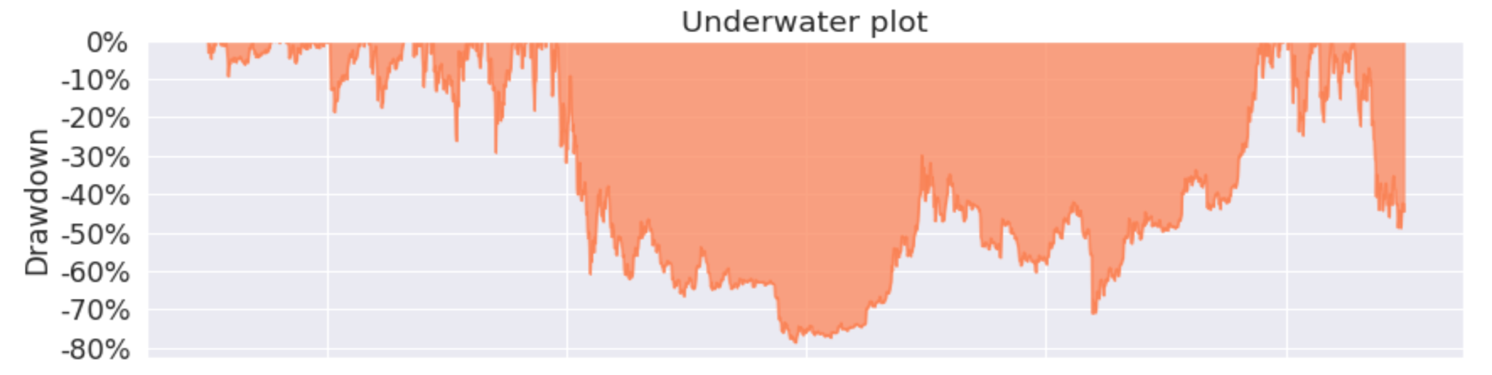
Com ele podemos ver melhor a utilidade desta análise, para visualizar as piores perdas passadas de um ativo ou portfólio. No caso do Bitcoin fica claro que um investidor que deseja investir neste ativo deve estar disposto a passar por períodos de muita volatilidade, enfrentando forte quedas constantemente.
Stress Test
O Stress Test é um processo amplo que pode ser aplicado a um portfólio de investimentos, com o objetivo de verificar como que os ativos seriam afetados de acordo com cenários adversos.
O Stress Test pode ser usado com o intuito de avaliar o desempenho do portfólio como um todo em cenário de instabilidade, e para avaliar o desempenho dos ativos individualmente, e assim permitir analisar quais ativos dentro do portfólio seriam os mais sensíveis a instabilidades no mercado.
Para o portfólio em questão foi aplicado um Stress Test histórico, onde aplicamos o portfólio atual em crises passadas. Os cenários passados utilizados podem ser crises econômicas, políticas, momentos de incerteza sobre o mercado, basicamente qualquer cenário que possa impactar os ativos dentro do portfólio.
Foram selecionados 3 períodos de fortes quedas do mercado e comparado os desempenhos hipotéticos do portfólio nessas quedas, frente ao desempenho que o Ibovespa teve nesses períodos.
Os períodos selecionados foram: o impacto da crise de 2008 na bolsa brasileira, o Joesley Day que ocorreu em 2017 e mais recente, a chegada da pandemia do corona vírus no Brasil em março de 2020.
No gráfico e tabela abaixo temos os resultados da aplicação, e podemos ver que o portfólio não se distanciou muito do desempenho do Ibovespa em nenhuma das situações. O que já era de se esperar, pois o portfólio é composto por algumas das maiores ações do índice.
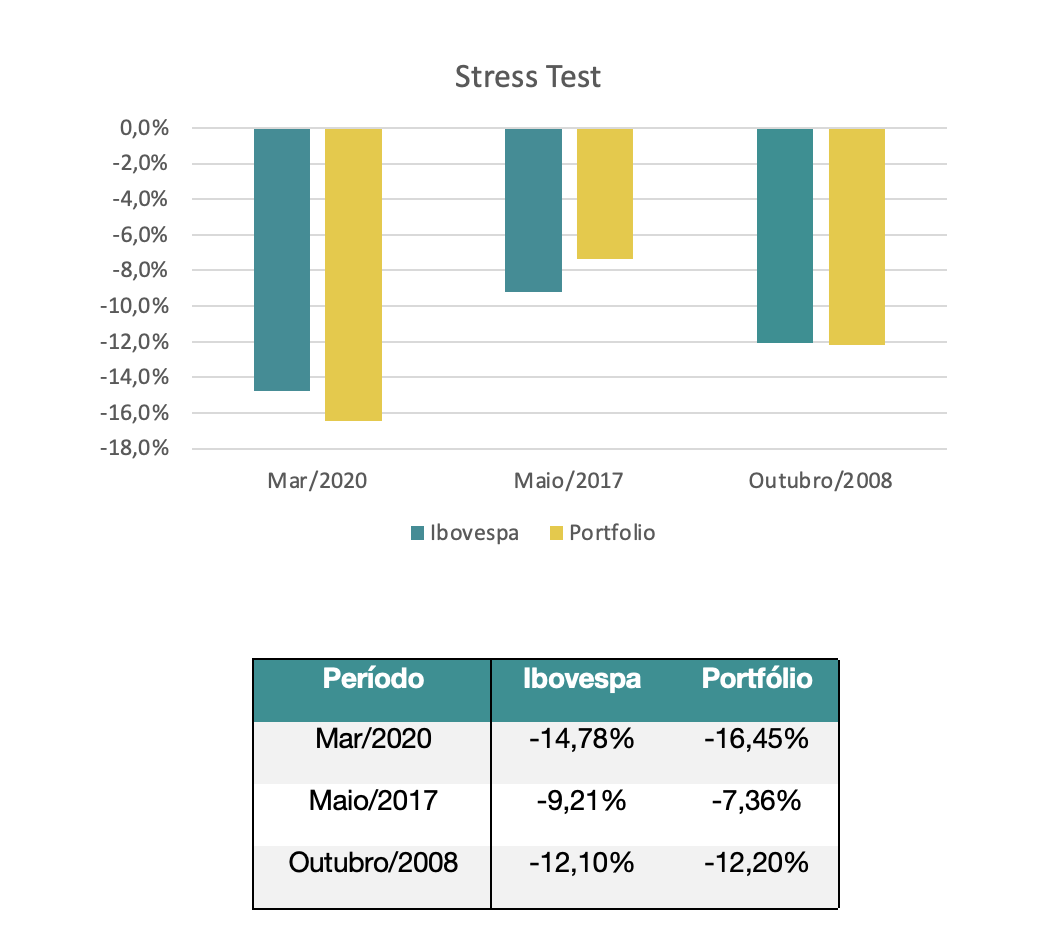
Com os resultados do Stress Test obtidos, é possível estabelecer as chamadas Políticas de Resposta. É através delas que, a partir da identificação dos principais pontos fracos do portfólio, buscamos aplicar medidas a fim de fortalecer a carteira, seja com um rebalanceamento do portfolio ou um Hedge com derivativos no mesmo.
Referências
Alexander, Carol. And Sheedy, Elizabeth. The Professional Risk Manager’s Handbook: A Comprehensive Guide to Current Theory and Best Practices. 1 ed. PRMIA Publications, 2005.
JORION, Philippe. Financial Risk Manager Handbook. 3. ed. New Jersey: John Wiley & Sons Inc, 2007
JORION, Philippe. Portfolio Risk: Analytical Methods. Value At Risk: The New Benchmark for Managing Financial Risk. 3. ed.