Rafael F. Bressan

Foi membro do Clube de Finanças Esag e gerente do núcleo de pesquisa em riscos e derivativos, no período 2018 a 2019. Bacharel em Ciências Econômicas pela UDESC/Esag. Aluno do mestrado acadêmico em Economia na FGV/EESP.

Jan

2019

Smile de Volatilidade parte 2

2019/01/25

Daremos continuidade ao artigo anterior sobre o smile de volatilidade. Falaremos sobre a estrutura a termo da volatilidade implícita, agregando uma segunda dimensão ao smile e transformando-o na famigerada superfície de volatilidade implícita. Também será definida o que é a arbitragem estática e seus tipos e como a limitação da presença de arbitragem estática impõe restrições na superfície de volatilidade. Por fim, será demonstrado como, a partir de um smile de volatilidade é possível derivar a distribuição implícita neutra ao risco do subjacente para data de expiração das opções.

Estrutura a termo

O mercado precifica a volatilidade implícita de forma que esta dependa também do tempo até expiração, bem como do preço de exercício.

A volatilidade implícita tende a ser uma função crescente da maturidade quando as volatilidades de curto prazo são historicamente baixas e função decrescente da maturidade quando as volatilidades de curto prazo são historicamente altas. Isso porque existe uma expectativa de reversão a uma média de longo prazo embutida na volatilidade. Esta característica é explorada explicitamente por alguns modelos de volatilidade, como em Heston (1993).

As superfícies de volatilidade combinam smiles com a estrutura a termo de volatilidade para tabular valores apropriados para precificar uma opção com qualquer preço de exercício e prazo de expiração.

Da mesma forma como a curva de juros em um dado momento é uma descrição concisa dos preços dos títulos negociados naquele mercado, assim, para um ativo subjacente em particular em determinado momento, a superfície de volatilidade implícita fornece uma descrição resumida de seu mercado de opções. Considerando que os rendimentos dos títulos são diferenciados pelo seu tempo até o vencimento, as opções são diferenciadas por seu tempo até a expiração e o strike, logo requerem uma superfície ao invés de uma curva.

A figura 1 demonstra uma superfície de volatilidade implícita do SPX em 15/09/2005, conforme apresentado em Gatheral (2011).

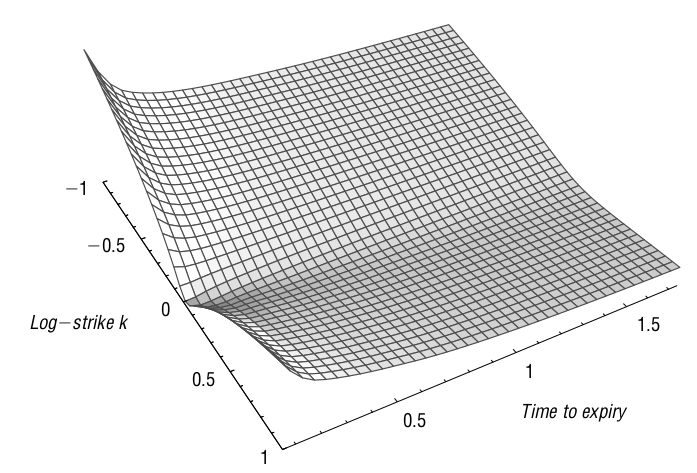
Figura 1: Superfície de volatilidade implícita.

Arbitragem estática

Antes de definir o que é arbitragem estática que pode estar presente em uma superfície de volatilidade (ou na superfície de preço de opções), vamos partir para a intuição por trás desta definição.

O princípio de ausência de arbitragem é dominante na teoria financeira. Este princípio nos informa que não deve existir lucro sem que se incorra em algum tipo de risco, o lucro sempre é a remuneração do investidor que aceitou carregar alguma forma de risco durante o investimento. Portanto, não devem existir perfis de lucro acima da taxa livre de risco (payoffs positivos) com probabilidade de 100%.

Primeiro consideramos uma trava de alta com opções do tipo call. Excluindo-se os custos de transação, esta operação sempre oferece um retorno positivo ou zero, conforme a figura 2. Por mais que esta estratégia esteja montada fora do dinheiro, sempre existe uma possibilidade de ela ter lucro, $S_T>K$ e portanto seu preço deve ser sempre maior que zero.

Figura 2: Perfil de lucro de uma trava de alta.

É claro que quanto mais ITM estejam as opções, maior seu preço e quanto mais fora do dinheiro menor será seu valor até o limite inferior zero. Se levarmos a diferença entre os strikes, $dK$ a zero temos que:

\[\frac{\partial C}{\partial K}\leq 0\]

Este é o limite de arbitragem para travas de alta ou, mais conhecido pelo termo em inglês call spread no-arbitrage e impõe que os preços das calls devem ser uma função descrescente no strike. De forma equivalente e através da paridade compra-venda este limite de arbitragem para as puts é:

\[\frac{\partial P}{\partial K}\geq 0\]

Arbitragem de borboleta

Também deve ser imposta uma restrição na segunda derivada do preço das opções em relação ao strike, e esta é conhecida como limite de arbitragem para borboletas. Vejamos porquê.

Considere uma estratégia do tipo borboleta, onde se compra uma quantia de calls no strike $K-dK$, vende-se duas vezes esta quantia em $K$ e compra-se novamente um lote em $K+dK$, o perfil de lucro desta operação no vencimento está representado na figura 3.

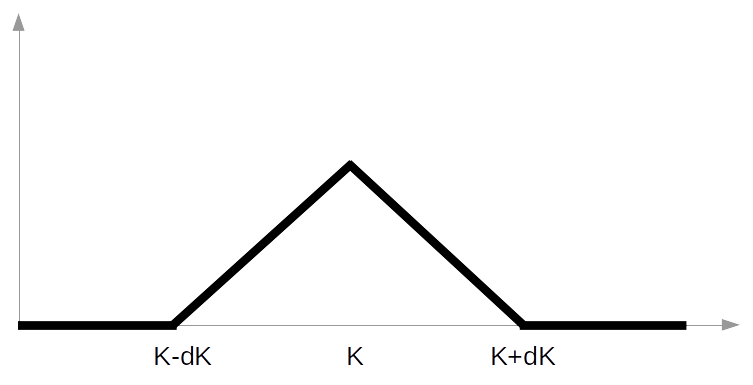
Figura 3: Borboleta realizada com calls.

Seguindo a mesma linha de raciocínio anterior, como o payoff da borboleta é sempre não negativo também deve ser o seu valor para qualquer período anterior a expiração. Se denotarmos $\pi_B$ o valor da borboleta, então $\pi_B\geq0$.

Agora imagine que escalamos a estratégia de forma que um lote de compras (na venda são dois lotes) seja de tamanho $1/dK^2$, o valor para a montagem desta operação deve ser, portanto:

\[ \pi_B=\frac{C(K-dK)-2C(K)+C(K+dK)}{dK^2} \]

E se levarmos ao limite em que $dK\rightarrow 0$, a equação acima torna-se justamente a segunda derivada do preço da call no strike $K$.

\[ \begin{aligned} \frac{\partial^2 C(K)}{\partial K^2}=& \pi_B\\ \geq & 0 \end{aligned} \]

Ou seja, os preços das calls são uma função convexa nos strikes. O mesmo raciocínio pode ser feito para uma borboleta com puts e o resultado será equivalente, o preço das puts também deve ser uma função convexa nos strikes.

Arbitragem de calendário

Passamos agora a analisar os limites de arbitragem na estrutura a termo da superfície de volatilidade. A arbitragem de calendário normalmente é expressa em termos de monotonicidade dos preços em relação ao período para expiração. Ou seja, quanto maior o prazo de maturidade de uma opção para um mesmo preço de exercício, maior deve ser seu valor.

É fácil de entender este limite com base nas probabilidades de exercício. Como sabemos, em um processo estocástico do tipo MBG a variância do processo cresce conforme a raiz do tempo, $\sqrt{\tau}$. Quanto maior a variância do ativo subjacente, maior a probabilidade deste alcançar um determinado preço, mais elevado ou não. Assim, seja uma call ou put OTM quanto mais distante estiver seu prazo de maturidade, maior a probabilidade de exercício e portanto, maior seu valor.

Dado que a relação de volatilidade total implícita e preço de uma opção também é direta e positiva, conforme demonstrado na parte 1 deste artigo, segue que a volatilidade total deve ser não decrescente no tempo para expiração.

Esta relação pode ser expressa através da seguinte equação para uma call precificada através de B&S:

\[ \frac{\partial C_{BS}(k, \theta(\tau))}{\partial \tau}=\partial_\theta C_{BS}\cdot\partial_\tau \theta \geq 0 \]

onde $\partial_\theta C_{BS}$ é a derivada parcial do preço da call em relação a volatilidade total implícita, que já demonstramos ser positiva e $\partial_\tau \theta$ é a derivada parcial da volatilidade total implícita em relação ao tempo para maturidade que, portanto, deve ser maior ou igual a zero para obedecer a restrição imposta ao preço da call.

Limites de inclinação

Se mantivermos a volatilidade implícita constante para todos os strikes, os preços das calls no modelo B&S devem ser decrescentes. Por outro lado, para um strike fixo, o preço de uma call se eleva à medida que a volatilidade implícita aumenta. Suponha por um momento que a volatilidade implícita varia com o strike como é o caso nos smiles. À medida que o strike aumenta, se a volatilidade implícita aumentar muito rapidamente, seu efeito sobre o preço da call pode mais que compensar o declínio no preço devido a elevação do preço de exercício e, assim, levar a um aumento líquido no preço da opção. Isso violaria o requisito de que $\partial C /\partial K \leq 0$ e, portanto, leva a um limite superior na taxa em que a volatilidade implícita pode aumentar com o strike.

Novamente, o mesmo raciocínio pode ser imposto para o lado das puts. A volatilidade implícita não pode se elevar tão rapidamente quando os strikes se reduzem de forma que uma put de strike menor tenha valor mais elevado que outra que esteja mais próxima do dinheiro.

Finalmente, um sumário dos limites impostos a uma superfície de preços de opções (calls no caso apresentado), que implicam em limites para a superfície de volatilidade é apresentado abaixo¹:

$\partial_\tau C \geq 0$
$\lim\limits_{K\rightarrow\infty}C(K, \tau)=0$
$\lim\limits_{K\rightarrow-\infty}C(K, \tau)+K=a, \quad a \in \mathbb R$
$C(K, \tau)$ é convexa em $K$
$C(K, \tau)$ é não-negativa

Distribuição implícita

O modelo B&S é baseado na suposição que o ativo subjacente segue uma distribuição log-normal em seus preços. Caso esta suposição fosse de fato realizada no mercado, o smile de volatilidade seria uma reta completamente horizontal, não haveria variação na volatilidade implícita conforme o preço de exercício. Entretanto, esta não é a realidade dos smiles e podemos fazer a pergunta inversa portanto, qual a distribuição neutra ao risco que está implícita no smile de volatilidade?

Certamente não é uma log-normal. Na verdade, a densidade da distribuição que está implícita em um smile nada mais é que a convexidade deste smile, ou seja, sua segunda derivada em relação ao strike. Esta distribuição implícita também é por vezes chamada de RND (risk neutral density) e é muito útil para fazer a precificação de outras opções que não são observadas no smile ou extrair probabilidades de ocorrência de eventos precificadas pelo mercado.

Pode-se obter este resultado a partir da definição do valor de uma call e é conhecido como a fórmula de Breeden-Litzenberger². O valor de uma call é o valor esperado do payoff terminal desta call ponderado pela densidade neutra ao risco do subjacente. Ou seja:

\[ C(S, t)=e^{-r\tau}\int\limits_{0}^\infty p(S,t,S_T,T)\max\{S_T-K, 0\}dS_T \]

onde $p(\cdot)$ é a densidade neutra ao risco e estamos supondo uma taxa de juros livre de risco constante durante o período de vida da opção. Como o payoff da call é não linear, sendo zero para qualquer valor de $S_T \leq K$ e igual a $S_T-K$ quando $S_T > K$, podemos escrever esta equação como:

\[ C(S, t)=e^{-r\tau}\int\limits_{K}^\infty p(S,t,S_T,T)(S_T-K)dS_T \]

que pode ser rearranjada, com alguma simplificação na notação, da seguinte forma.

\[ \begin{aligned} \frac{\partial C}{\partial K}=& -e^{-r\tau}\int\limits_{K}^\infty p(S_T)dS_T\\ e^{r\tau}\frac{\partial C}{\partial K}=& \int\limits_{-\infty}^K p(S_T)dS_T\\ e^{r\tau}\frac{\partial^2 C}{\partial K^2}=& \ p(K)\\ \frac{\partial^2 C_B}{\partial K^2}=& \ p(K)\\ \end{aligned} \]

Onde usou-se a notação $C_B$ para denotar a formulação de Black para o preço de uma call. Ou seja, a segunda derivada em relação ao strike do preço não descontado de uma call é a distribuição neutra ao risco do ativo subjacente, e é válida para todos preços de exercício.

Portanto, se desejarmos saber qual a distribuição de probabilidades de preços do ativo subjacente em uma data futura que possua vencimento de opções, basta encontrarmos a convexidade do smile dos preços forward daquele vencimento³.

Conclusão

Este foi um artigo denso, porém com vários conceitos importantes para a compreensão do comportamento da superfície de volatilidade. A estrutura a termo também é existente na volatilidade implícita e está limitada pela ausência de arbitragem do tipo calendário. O smile de volatilidade, que é uma fatia da superfície com prazo de expiração constante, possui suas próprias limitações de forma, com a ausência de arbitragem do tipo borboleta e limitações quanto a inclinação.

Por fim, foi demonstrado como a convexidade do smile de preços fornece a distribuição implícita para os preços do ativo subjacente para a data de expiração das opções.

Referências

Aurell, Alexander. 2014. “The Svi Implied Volatility Model and Its Calibration.” Master’s thesis, Kungliga Tekniska Högskolan.

Breeden, Douglas T, and Robert H Litzenberger. 1978. “Prices of State-Contingent Claims Implicit in Option Prices.” Journal of Business. JSTOR, 621–51.

Gatheral, Jim. 2011. The Volatility Surface: A Practitioner’s Guide. Vol. 357. John Wiley & Sons.

Heston, Steven L. 1993. “A Closed-Form Solution for Options with Stochastic Volatility with Applications to Bond and Currency Options.” The Review of Financial Studies 6 (2). Oxford University Press: 327–43.

Retirado de
Aurell (2014), p. 25.[↩][2]

Autores da formulação em seu artigo,
Breeden and Litzenberger (1978)[↩][3]

Simples em teoria, muito mais complicado na prática, com diversos problemas para a extrapolação do smile para strikes extremos.↩

Jan

2019

Smile de Volatilidade

<br /> Smile de Volatilidade – Superfície de Volatilidade<br />

2019/01/18

A volatilidade instantânea, $\sigma$, do ativo subjacente é a única variável no modelo B&S que não pode ser diretamente observada. De fato, a volatilidade (ou equivalentemente a variância) de um ativo é dita uma variável latente. Sabemos que ela existe e possui algum valor no processo gerador, o processo pelo qual os preços são formados, porém não conseguimos observá-la diretamente, apenas estimá-la. Uma das formas de estimação de volatilidade pode ser a partir de dados históricos, mas várias outras formas existem, entre elas processos GARCH, volatilidade realizada, volatilidade estocástica, etc.

Uma vez que a volatilidade não pode ser diretamente observada, a prática comum no mercado é fazer o caminho inverso. Considerar os preços de mercado para as opções como dado, e a partir do modelo B&S inverter a equação de preço da Call ou Put para encontrar a volatilidade deste modelo que é compatível com os preços de mercado. A esta volatilidade encontrada damos o nome de volatilidade implícita.

Portanto, o smile de volatilidade que tratamos neste post é na verdade um gráfico entre a volatilidade implícita, retirada de opções Européias (baunilhas, do inglês vanilla options) a partir do modelo B&S, contra os strikes destas opções.

Reparametrizando B&S e definição de moneyness

Nem sempre é interessante plotar o smile contra os strikes propriamente ditos, uma forma de avaliar o quanto uma opção está “dentro, fora ou no dinheiro” pode ser a grega Delta ou então o chamado moneyness (por favor, se alguém tiver uma boa tradução para este termo, deixe nos comentários). Tradicionalmente a medida de moneyness é a relação $K/S$, ou seja o strike contra o preço corrente do subjacente. Porém existem outras definições mais interessantes para se trabalhar, entretanto, antes devemos fazer uso de algumas definições e vamos reparametrizar as expressões $d1$ e $d2$ do modelo B&S.

Lembrando que em precificação de opções estamos no mundo neutro ao risco, vamos definir o valor forward, $F$ do subjacente como o valor corrente composto pela taxa livre de risco até a maturidade da opção, ou seja:

\[F=e^{r\tau}S\]

A volatilidade (implícita) total pode ser definida como a volatiliade reescalada pela raiz do tempo, que nos dá uma informação da volatiliade esperada para o subjacente do período corrente até a maturidade. Da mesma forma, a variância total. Denotanto a volatilidade total por $\theta$ e a variância total por $w$, temos:

\[\theta=\sigma_{imp}\cdot \sqrt{\tau}\]

\[w=\sigma_{imp}^2\cdot\tau\]

Vamos também definir a medida forward log-moneyness e denotá-la por $k$. Esta será a medida de moneyness que iremos utilizar ao longo deste e de outros artigos, portanto iremos utilizar este termo para designar o forward log-moneyness a não ser que expresso de forma contrária no texto.

\[k=\ln\left(\frac{K}{S}\right)-r\tau=\ln\left(\frac{K}{F}\right)\]

Logo, o strike está relacionado ao moneyness de forma que: $K=Fe^k$.

Podemos agora reparametrizar as expressões $d1$ e $d2$ do modelo B&S de forma que serão mais facilmente trabalhadas em modelos de volatilidade. Lembrando destas expressões que já foram apresentadas em artigo anterior:

\[\begin{aligned} &d_{1}={\frac {\ln(S/K)+(r+\sigma ^{2}/2)(\tau)}{\sigma {\sqrt {\tau}}}}\\ &d_{2}={\frac {\ln(S/K)+(r-\sigma ^{2}/2)(\tau)}{\sigma {\sqrt {\tau}}}}=d_1-\sigma\sqrt{\tau} \end{aligned}\]

Substituindo as expressões para forward log-moneyness e volatilidade total nas definições acima temos as novas parametrizações para $d1$ e $d2$:

\[\begin{aligned} &d_{1}={-\frac{k}{\theta}+\frac{\theta}{2}}\\ &d_{2}={-\frac{k}{\theta}-\frac{\theta}{2}}=d_1-\theta \end{aligned}\]

Retomando o valor da opção do tipo Call no modelo B&S, podemos reescrever sua fórmula de apreçamento da seguinte forma:

\[\begin{aligned} C(K, \tau)=&SN(d1)-Ke^{-r\tau}N(d2)\\ e^{r\tau}C(K, \tau)=&FN(d1)-KN(d2)\\ =&F\left[N(d1)-e^kN(d2)\right] \end{aligned}\]

Esta equação é conhecida como a forma de Black de precificação (Black Call price formula), que relaciona os valores forward da opção (também conhecido como valor não descontado), do subjacente e do strike. Esta formulação é particularmente útil quando formos extrair a distribuição neutra ao risco do subjacente que está implícita nos preços de mercado das opções.

Características de smiles de volatilidade

Caso o modelo de Black, Schole e Merton estivesse em acordo com a realidade, e os ativos tivessem seus preços formados a partir de um verdadeiro MBG, a volatilidade implícita seria uma constante. O gráfico do smile de volatilidade seria uma reta horizontal, com a mesma volatilidade para qualquer nível de moneyness e se considerarmos a superfície toda (que leva em conta os diversos tempos para expiração) esta seria paralela ao domínio $(k, \tau)$. Não estaríamos escrevendo (e você lendo) este artigo se este fosse o caso…

O fato é que o modelo B&S é um modelo muito restritivo, com inúmeras suposições que não se verificam no mundo real e que por conseguinte, tornam os resultados do modelo pouco acurados. Entretanto este é um modelo muito conhecido, de fácil assimilação por parte dos agentes de mercado e que virou a língua franca nos mercados de derivativos. Se todos os traders conversarem em termos do modelo B&S, todos se entenderão, mesmo que internamente cada um possua seu próprio modelo de apreçamento.

Entre as características tipicamente observadas em smiles (e superfícies) de volatilidades pode-se citar:

As volatilidades implícitas variam conforme o strike e prazo de expiração
Smiles apresentam skew. Maior inclinação em uma das asas, representando uma maior probabilidade daqueles strikes acontecerem
Smiles de equity tipicamente são negativos
Mercados diferentes apresentam padrões de smile diferentes

Mercados cambiais

Opções sobre moedas possuem tipicamente um smile de volatilidade conforme mostrado na figura 1 abaixo. A volatilidade implícita é relativamente baixa para opções ATM. Esta torna-se progressivamente maior quando a opção se move para dentro do dinheiro ou para fora.

Figura 1: Smile de volatilidade típico de um mercado cambial.

Caso a distribuição dos preços do ativo subjacente, neste caso uma taxa de câmbio fosse perfeitamente log-normal como no modelo B&S, o smile não teria esta curvatura. Desta forma podemos afirmar que o mercado, ao precificar as opções, acredita que a distribuição deste ativo possui caudas com maior densidade que supõe a log-normal, existem maiores probabilidades de retornos muito baixos ou muito altos.

Mercados de equities

Nos mercados de equities, ações, índices de ações e ETFs, por exemplo, o smile apresenta uma característica de assimetria (skew, em inglês) negativa. A asa esquerda (parte onde as puts estão fora do dinheiro) apresenta valores de volatilidade implícita muito maiores que suas contrapartes no lado das calls. Este comportamento reflete a percepção de mercado de uma maior probabilidade de grandes perdas nas ações que altos ganhos, gerando portanto, uma distribuição de preços assimétrica. Como existe uma maior probabilidade de perdas extremas, o seguro para estas, ou seja, uma put é relativamente mais cara que uma call.

Figura 2: Smile de volatilidade típico de uma ação ou índice de ações.

Smile como forma de precificação

Analisando a equação de B&S com a parametrização para $d1$ e $d2$ dada no início deste artigo é possível verificar que existe uma relação direta entre volatilidade implícita e preço de uma opção, seja esta uma call ou put.

Como $d1$ é estritamente crescente em $\theta$ e $d2$ é estritamente decrescente e ao mesmo tempo o preço de uma opção é crescente em d1 e decrescente em d2, logo, temos uma relação direta entre o preço de uma opção e sua volatilidade implícita para uma dada maturidade. Em outras palavras, em um smile, tudo o mais constante, quanto maior a volatilidade implícita maior o preço da opção naquele strike.

Outra forma de verificar esta relação é perceber que a grega Vega, que é calculada da mesma forma para calls e puts, é sempre positiva. Ou seja, um aumento no valor da volatiliade sempre leva a elevações no preço de uma opção.

Desta forma é normal entre os praticantes de mercado fazer a precificação de opções em termos de “pontos de volatilidade” e não em valores monetários propriamente ditos. Isto porque o modelo B&S, apesar de não ser o modelo correto (nenhum é) para a precificação de opções, é conhecido e de fácil entendimento para todos. Então todos os praticantes podem fazer suas cotações em termos de volatilidades implícitas, que são extraídas de opções baunilhas com o modelo B&S, e somente na hora de fechar um negócio e liquidar o pagamento, o preço efetivo a ser pago é acordado entre as partes.

Conclusão

O modelo de Black-Scholes-Merton, pode ser considerado a pedra fundamental para a precifição de opções. Entretanto, este modelo apresenta uma séries de limitações que fazem com que os praticantes de mercado utilizem outras técnicas neste mercado. Uma destas é o uso do smile de volatilidade e sua interpretação como forma de precificar opções e extrair informações implícitas nos preços.

A assimetria do smile e suas asas informam que as distribuições de probabilidades para o ativo subjacente não são exatamente log-normais, e podem apresentar discrepâncias significativas, especialmente nas caudas da distribuição que muito interessam a gestão de risco, por exemplo.

Oct

2018

O Modelo Black-Scholes-Merton

Clique no link abaixo para abrir o post.

Modelo Black-Scholes-Merton

Sep

2018

Simulação de Monte Carlo

Em artigo anterior, sobre processos estocásticos, fizemos uso de uma poderosa ferramenta computacional, frequentemente utilizada em finanças para fazer simulações. Naquele artigo simulamos cinco realizações de caminhos de um processo estocástico, cada um com 500 passos a frente. Esta técnica é conhecida como Simulação de Monte Carlo – SMC e será abordada no presente artigo.

Neste artigo também iremos introduzir, no corpo do texto, os códigos em linguagem R utilizados para fazer as simulações, aumentando a didática de nossos artigos. A linguagem R é uma das preferidas para a modelagem estatística, é uma das linguagens de ciência de dados que vem ganhando muitos adeptos e, por conseguinte, é amplamente utilizada pelo mercado financeiro. E claro, é uma das preferidas aqui do CF também.

Nosso problema será simular a posição de um portfólio composto por uma posição comprada em uma ação PETR4 e uma put PETRV17. A opção de venda (put) tem preço de exercício em R$ 16,92, data de expiração em 15/10/2018 e é do tipo europeia. Ao final do pregão do dia 21/09/2018 a ação PETR4 fechou cotada a R$ 20,14 e a put em R$ 0,12. A partir desta data até o dia da expiração da opção haverão 16 dias de pregão, que será nosso horizonte de simulação.

Para melhoria da didática do texto e também para simplificação do problema, manteremos algumas variáveis necessárias para a precificação de opções constantes ao longo do período de análise, são elas:

Volatilidade: Será calculada a volatilidade implícita da opção da data de compra do portfólio, 21/09/2018, e será mantida constante a partir daí para fins de precificação na SMC;
Taxa de juros: constante no valor de 6,5 %a.a. tem termos contínuos;
Taxa de dividendos: suposto igual a zero.

Simulação de Monte Carlo

Para realizar uma SMC de um ativo financeiro deve-se primeiramente estabelecer uma distribuição de probabilidades que os retornos deste ativo deve seguir. Em nosso exemplo, utilizaremos a distrbuição normal para os retornos logarítimicos da ação PETR4, em linha com o clássico modelo Black & Scholes, certamente existem diversas variantes que se ajustam melhor a realidade dos mercados, entretanto este é o modelo mais conhecido e base de todos os demais.

Uma vez escolhida a distribuição dos (log) retornos, tem-se de escolher valores para a média e variância desta distribuição. A média dos retornos iremos tirar do histórico da ação, o retorno médio diário dos último ano. A variância da distribuição será encontrada a partir da volatilidade implícita da opção na data de compra do portfólio. A função utilizada para encontrar esta volatilidade retorna um valor em termos anuais, portanto, conforme visto no artigo sobre processos estocásticos devemos reescalar uma volatilidade anual para diária, e isto é obtido fazendo a divisão por (\sqrt{252}), onde temos 252 dias úteis em 1 ano.

Desta forma é possível fazer a simulação dos log-retornos da ação para cada um dos dias a frente, até a data de exercício da opção, 15/10/2018. Estes retornos são acumulados e o preço simulado da ação PETR4 em uma data intermediária é o preço de compra vezes o retorno acumulado até então.

Faremos 1.000 simulações destas, gerando caminhos possíveis de preços para a ação. É necessário fazer muitas simulações para termos uma boa ideia da distribuição dos preços na data final, não é raro serem feitas mais de mil simulações, as vezes até dez mil podem ser necessárias.

Uma vez gerados todos os caminhos simulados do preço do ativo objeto, podemos então precificar a put com base nestes preços simulados e as outras variáveis necessárias para se precificar uma opção europeia. Assim teremos também todos os caminhos de preço para a opção até sua data de exercício.

O valor de nosso portfólio, em qualquer ponto do intervalo de tempo em análise, será a soma do preço da ação com o preço da opção e será possível verificar o efeito de proteção contra quedas do preço do ativo objeto a compra da put tem no portfólio.

Cabe ressaltar aqui que o preço da opção não é simulado, não diretamente. Como a opção é um instrumento derivativo o seu preço “deriva” do preço do ativo objeto, este sim que é simulado. Uma vez que tenhamos o preço da ação, dadas nossas premissas de precificação, podemos calcular o prêmio da opção com base no modelo Black & Scholes.

Implementação em R

Conforme comentado, utilizamos aqui no CF a linguagem de programação R para realizar nossas atividades que envolvam métodos quantitativos em finanças. Abaixo irei apresentar o código utilizado, trecho a trecho e o resultado obtido ao final.

Primeiramente, no R, devemos carregar em nossa sessão de trabalho os pacotes que serão utilizados ao longo do código. Os pacotes funcionam como extensões ao R base, nestes pacotes encontramos diversas funções já programadas por outras pessoas que facilitam (e muito!) a nossa codificação.

library(tidyverse)
library(ggthemes)
library(tidyquant)
library(RQuantLib)

O pacote RQuantLib, por exemplo, possui já implementado dentro dele funções para fazer a precificação de opções europeias, sem que se tenha que implementar o modelo manualmente. Como a intenção deste artigo não é explicar o modelo Black & Scholes, vamos abstrair esta parte e simplesmente chamar uma função que nos retorna o valor da opção dadas as variáveis de entrada.

Em seguida iremos definir algumas de nossas variáveis, como o ticker da ação para buscar seus dados históricos através da função tq_get() do pacote tidyquant e calcular os retornos logarítimicos e tirar sua média, o preço e data de exercício da opção e também iremos relacionar os dias de negócio entre a data de compra e vencimento.

acao <- "PETR4.SA"
p_exer <- 16.92
d_exer <- as.Date("2018-10-15")
d_atual <- as.Date("2018-09-21")
dias <- seq(d_atual, d_exer, by = 1)
dias <- dias[isBusinessDay("Brazil", dias)]
nsims <- 1000
ndias <- length(dias) - 1
sim_nomes <- paste0("sim", 1:nsims)

# Carregar os precos historicos da acao
p_hist <- tq_get(acao, from = d_atual - years(1), to = d_atual + days(1)) %>% 
  filter(volume != 0.0)
ret_hist <- p_hist %>% 
  tq_mutate(select = adjusted,
            mutate_fun = periodReturn,
            period = "daily",
            type = "log",
            leading = FALSE,
            col_rename = "log_ret") %>% 
  na.omit()
rf <- log(1 + 0.065)
div <- 0
S0 <- last(ret_hist$adjusted)
P0 <- 0.12
mi <- 252 * mean(ret_hist$log_ret) # retorno medio em termos anuais
sigma <- EuropeanOptionImpliedVolatility("put", P0, S0, p_exer, div, rf, 
                                         (ndias + 1) / 252, 0.30)

Com o código acima obtemos basicamente todos os dados com os quais poderemos implementar a simulação de Monte Carlo. Entretanto, para realizar as simulações, necessitamos especificar mais algumas funções customizadas para nossas necessidades.

Primeiro iremos especificar uma função que retorna uma única simulação de log-retornos acumulados em uma coluna de dados, esta função é chamada de mc_sim_fun. A segunda função necessária é a função de precificação da opção europeia. Por padrão, a função do pacote RQuantLib EuropeanOption() retorna uma lista com o valor da opção, mas também todas as suas gregas. Também de forma um tanto quanto estranha, esta função retorna o valor zero na data de exercício, mesmo que a opção esteja In-The-Money, portanto é necessário modificar este comportamento.

# Funcao para realizar uma simulacao
mc_sim_fun <- function(valor_i, N, media, volat){
  med_d <- media / 252
  volat_d <- volat / sqrt(252)
  ans <- tibble(c(valor_i, rnorm(N, med_d - (volat_d^2 / 2), volat_d))) %>% 
    `colnames<-`("log_ret") %>%
    mutate(ret_ac = cumsum(log_ret)) %>% 
    select(ret_ac)

  return(ans)
}

# Funcao para precificar uma opcao europeia
eur_option <- function(type, underlying, strike, dividendYield, riskFreeRate, 
                       maturity, volatility) {
  if (maturity == 0.0) {
    ans <- switch(type,
                  put = max(strike - underlying, 0),
                  call = max(underlying - strike, 0))
    return(ans)
  }

  ans <- EuropeanOption(type = type,
                        underlying = underlying,
                        strike = strike,
                        dividendYield = dividendYield,
                        riskFreeRate = riskFreeRate,
                        maturity = maturity,
                        volatility = volatility)$value
  return(ans)
}

Uma vez com os dados obtidos e as funções auxiliares programadas, podemos passar a SMC propriamente dita. Aqui vamos estabelecer o número de simulações (1.000), calcular um data frame com os log-retornos acumulados e então calcular o preço da ação para cada dia e simulação realizados. O preço da ação na data (t) será (S_t=S_0 e^{r_t}), onde (r_t) é o log-retorno acumulado até a data (t).

Após termos todos os preços do ativo objeto, passamos a computar qual seria o preço da opção, (P_t), naquelas condições. O valor do portfólio é dado pela soma destes dois preços (lembre-se, nosso portfólio é composto por uma ação e uma opção de venda).

# Simulacao de Monte Carlo
# Valores Iniciais
inic <- rep(0, nsims) 
set.seed(12345)
ret_ac_mc <- map_dfc(inic,
                     mc_sim_fun,
                     N = ndias,
                     media = mi,
                     volat = sigma)

precos_acao <- (S0 * exp(ret_ac_mc)) %>% 
  set_names(sim_nomes) %>% 
  mutate(anos_exp = (ndias:0) / 252) %>% 
  gather(key = sims, value = St, -anos_exp)

# Evolucao do Portfolio
port_mc <- precos_acao %>% 
  mutate(Pt = map2_dbl(St, anos_exp, 
                       ~eur_option(type = "put",
                                   underlying = .x,
                                   strike = p_exer,
                                   dividendYield = div,
                                   riskFreeRate = rf,
                                   maturity = .y,
                                   volatility = sigma)),
         port_valor = Pt + St,
         data = rep(dias, nsims))
head(port_mc)

##     anos_exp sims       St         Pt port_valor       data
## 1 0.05952381 sim1 20.14000 0.10666291   20.24666 2018-09-21
## 2 0.05555556 sim1 20.56213 0.06610065   20.62823 2018-09-24
## 3 0.05158730 sim1 21.08354 0.03486500   21.11841 2018-09-25
## 4 0.04761905 sim1 21.01296 0.03001788   21.04297 2018-09-26
## 5 0.04365079 sim1 20.69410 0.03266826   20.72677 2018-09-27
## 6 0.03968254 sim1 21.14278 0.01516756   21.15794 2018-09-28

O data frame port_mc contém todas as informações da SMC de nosso portfólio. Contém as datas desde o dia da compra até a data de vencimento da opção e contém todos os caminhos de (S_t), (P_t) e do portfólio. Vamos plotar os resultados obtidos para a evolução apenas da ação, primeiramente.

brk <- round(sort(c(p_exer, seq(min(port_mc$St),
                                max(port_mc$St),
                                length.out = 5))),
             digits = 2)
ggplot(port_mc, aes(x = data, y = St)) + 
  geom_line(aes(color = sims)) +
  geom_hline(yintercept = p_exer, color = "red") +
  guides(color = FALSE) +
  labs(title = "Simulações do Valor da Ação",
       x = "data",
       y = "Valor (R$)") +
  scale_y_continuous(breaks = brk) +
  scale_x_date(date_breaks = "2 days", date_labels = "%d") +
  scale_color_viridis_d() +
  theme_economist_white()

Podemos verificar pela figura acima que a ação, pela nossa SMC, deve fechar na maioria dos caminhos simulados acima do preço de exercício da put (linha vermelha). Entretanto existe uma menor probabilidade de, até a data de vencimento, o preço da ação cair abaixo do strike desta opção.

Podemos inferir esta probabilidade através do número de caminhos que terminaram em preço da ação abaixo do valor de referência. O custo de proteção contra este risco é o prêmio por nós ao comprarmos a put. O código para esta inferência está abaixo.

p_baixo <- port_mc %>% 
  filter(data == d_exer) %>% 
  summarise(num_baixo = sum(St < p_exer)) %>% 
  as.double()
prob <- p_baixo / nsims

Este cálculo nos mostra que em 82 caminhos simulados do preço de PETR4, este terminou abaixo do preço de exercío da opção PETRV17, ou seja, uma probabilidade de 8.2%.

Para nos precavermos desta possível queda de preço e garantir um valor mínimo de nosso portfólio até a data de 15/10/2018, podemos comprar uma opção de venda, com preço de exercício no valor que desejamos e então o portfólio passa a ser composto pela ação e também pela opção. Caso na data de vencimento o preço da ação seja menor que o preço de exercício da put, esta opção estará ITM e pode ser exercida pelo valor da diferença entre os preços, ou seja, nos garantindo que nosso portfólio estará avaliado em R$ 16,92.

Esta dinâmica pode ser verificada pela figura abaixo, que agora apresenta o valor do portfólio completo, ação mais opção. Verificamos que, de fato, no dia 15/10/2018 nosso investimento não estará em situação pior que o preço garantido pela compra da put.

brk <- round(sort(c(p_exer, seq(min(port_mc$port_valor),
                                max(port_mc$port_valor),
                                length.out = 5)[-1])),
             digits = 2)
ggplot(port_mc, aes(x = data, y = port_valor)) + 
  geom_line(aes(color = sims)) +
  geom_hline(yintercept = p_exer, color = "red") +
  guides(color = FALSE) +
  labs(title = "Simulações do Valor do Portfolio",
       x = "data",
       y = "Valor (R$)") +
  scale_y_continuous(breaks = brk) +
  scale_x_date(date_breaks = "2 days", date_labels = "%d") +
  scale_color_viridis_d() +
  theme_economist_white()

Ou seja, ao custo de 0.6% do preço da ação, compramos uma proteção contra uma queda de preços com probabilidade de 8.2%.

Esta é apenas uma (simples) aplicação das inúmeras possíveis que a Simulação de Monte Carlo possui no mundo das finanças. A SMC é uma poderosa ferramenta para avaliação e controle de risco de grandes portfólios, com centenas ou milhares de ativos, onde nem sempre consegue-se aferir medidas de retorno esperado ou de risco de mercado de forma analítica.

Sep

2018

Processos Estocásticos para Finanças: uma introdução

Neste artigo abordaremos um assunto técnico, mas muito utilizado e de fundamental importância para a precificação de instrumentos derivativos. Será apresentado o conceito de processos estocásticos – PE, e sua aplicação no mundo das finanças.

Um processo estocástico é a evolução temporal de uma determinada variável de interesse que pode assumir valores aleatórios em cada ponto no tempo. Em outras palavras, o caminho que a variável segue ao longo do tempo evolui de maneira incerta. Estes processos podem se dar em tempo discreto ou em tempo contínuo. Processo em tempo discreto são aqueles onde o valor da variável pode se alterar somente em intervalos pré-definidos de tempo, por exemplo ao final do dia. Em processos em tempo contínuo, o valor de nossa variável está constantemente em mudança, de forma aleatória seguindo alguma distribuição de probabilidades.

Estes processos são muito importantes em finanças pois, é amplamente aceito que a evolução do preço de ativos financeiros pode ser modelado por um PE em tempo contínuo, sendo este modelo portanto, a base para a teoria de precificação de ativos e da qual os derivativos fazem extenso uso. Aprender sobre a evolução temporal do preço de uma ação através de um processo estocástico é o primeiro passo para saber como atribuir um preço a uma opção sobre esta ação, por exemplo.

Deve ser notado também que apesar de o preço dos ativos serem observados apenas em intervalos discretos de tempo (apenas quando existe transação) e assumirem valores também discretos (múltiplos de um centavo), o preço e sua evolução estão ocorrendo continuamente, nossas observações que são discretas. Desta forma os processos em tempo contínuos são ideais para este tipo de modelagem.

Processos de Markov

Uma primeira definição de deve-se fazer para estudar PE aplicados a evolução do preço de ações é o conceito de processo de Markov. Este tipo de processo é tal que o histórico do processo que o levou até seu estado atual, é irrelevante para a previsão de seu estado futuro. Ou seja, toda a informação da história do processo já está contida no seu valor atual. Quando consideramos que preços de ativos seguem um processo de Markov, estamos assumindo válida pelo menos a forma fraca de mercados eficientes.

Uma implicação desta suposição, verificada empiricamente, é que não se pode obter lucros apenas seguindo padrões históricos do preço e extrapolando-os no futuro. Outra, mais importante para nossos processos, é que as distribuições de probabilidade que a variável aleatória segue em cada ponto no tempo são independentes.

Movimento Browniano

Suponha um processo de Markov, que para fins de simplificação consideraremos em tempo discretos. Se a distribuição de probabilidade para o próximo incremento no valor do processo for uma Normal com média zero e variância unitária, podemos representar este incremento por $\phi(0, 1)$. Como este é um processo de Markov, o segundo incremento será independente do primeiro e terá novamente a mesma distribuição de probabilidade. Qual seria então, a partir do período inicial até o segundo período, a distribuição de probabilidade dos possíveis valores de nosso hipotético processo? A reposta é a soma de duas normais $\phi(0, 1)$ que resulta em $\phi(0, 2)$. Se assim continuarmos a fazer previsões para T períodos a frente, nossa distribuição terá densidade $\phi(0, T)$.

Para tempos discretos, $T\in\mathbb{Z}$ este é o processo do passeio aleatório (Random Walk), entretanto para tempo contínuo quando $T\in\mathbb{R}$ com incrementos acontecendo em intervalos de tempo infinitesimalmente pequenos, este é o Movimento Browniano – MB, que também é largamente conhecido como processo de Wiener.

A figura acima mostra 5 realizações de um mesmo processo estocástico com média zero e variância unitária. É importante frisar que o processo que gerou as cinco séries é exatamente o mesmo, sendo elas tão distintas umas das outras ou não. Esta é uma importante característica dos processos estocásticos nas aplicações reais, o que nós observamos é apenas uma realização do processo, dentre as infinitas possíveis.

Definição

Agora que já foi passada a intuição sobre processos estocásticos, pode-se partir para definições mais formais sobre estes processos. Vamos adotar a notação do cálculo para tanto, e generalizar nosso MB possibilitando-o que tenha média diferente de zero $\mu$ e variância qualquer $\sigma^2$, mantendo estas constantes ao longo do tempo, entretanto. Desta forma um movimento Browniano com deriva pode ser descrito através da seguinte equação diferencial estocástica – EDE:

$$dX_t = \mu dt + \sigma dB_t$$

onde $dB_t$ é nosso MB padrão em um intervalo de tempo infinitesimal, $dt$.

O processo $X_t$ possui uma taxa de deriva (média instantânea) igual a $\mu$ e volatilidade instantânea igual a $\sigma$. Quando um PE possui deriva igual a zero, como nosso MB padrão, o valor esperado deste processo para qualquer período futuro será zero. Este fato deixa de ser verdade no processo generalizado, com taxa de deriva diferente de zero. Neste caso o processo evoluirá seguindo uma taxa crescente (se $\mu > 0$) ou decrescente (se $\mu < 0$). Assim é possível, a partir de um MB padrão, modelar outros PE que possuam tendência temporal e variâncias diferentes.

Movimento Browniano Geométrico

Apesar de o processo $X_t$ ser bastante flexível e cobrir uma grande gama de usos, ele ainda não é adequado para modelar o preço de ativos, e isto se dá em função de o processo de Wiener, mesmo com deriva positiva, poder atingir valores negativos com probabilidade maior que zero. Isto implicaria na possibilidade do preço de uma ação ser negativo, algo que obviamente não ocorre. Além desta impossibilidade, existe um outro empecilho para se utilizar o MB para modelar o processo de preços, e este é a deriva constante $\mu$ com relação ao preço da ação.

A deriva pode ser interpretada como o valor esperado do retorno da ação em um dado período de tempo. Este retorno esperado ele é pode ser constante em termos percentuais (em um modelo simplificado), mas não em termos absolutos! Ou seja, dependendo do preço da ação, R$ 1,00 ou R$ 100,00, a deriva $\mu$ deve ser diferente para que em termos percentuais a relação seja constante.

A solução para estes dois problemas é modelar o preço como um processo estocástico conhecido como Movimento Browniano Geométrico. Ele difere do MB padrão pois assume que o logaritmo da variável aleatória possui distribuição Normal. O MBG é a resolução para a seguinte EDE:

$$dX_t = \mu X_t dt + \sigma X_t dB_t$$

Veja que este é basicamente o mesmo processo MB, porém a deriva, termo que multiplica $dt$, varia linearmente com o valor do processo ($\mu X_t$) assim como a volatilidade instantânea ($\sigma X_t$).

A solução para esta EDE, para um valor inicial qualquer de $X (X_0 > 0)$ é dada por:

$$X_t = X_0\exp\left(\left(\mu-\frac{\sigma^2}{2}\right)t+\sigma B_t\right)$$

A variável aleatória $X$ segue um MB ao longo de uma trajetória exponencial. É fácil verificar que, por ser exponencial, $X_t$ nunca terá valor negativo.

Esta é uma forma conveniente de representar a evolução de preços de um ativo pois naturalmente surge o conceito de retornos logarítmicos. O log-retorno de $X$ é dado por $r_t=\ln(X_t/X_0)$ de onde inferimos que se o processo de formação de preço de um ativo segue um MBG, então seus log-retornos serão normalmente distribuídos com média $\mu-\frac{\sigma^2}{2}$ e volatilidade $\sigma$ em uma unidade de período considerado. Se escalarmos o período de tempo considerado para $T$, temos então que os retornos logarítmicos do ativo $X$ seguem a seguinte distribuição normal:

$$r_T \sim\phi\left(\left(\mu-\frac{\sigma^2}{2}\right)T, \sigma^2T\right)$$

Abaixo apresentamos 5 realizações de um MBG com valor de deriva $\mu = 0,6\% a.p.$ e variância $\sigma^2=1\% a.p.$.

O Movimento Browniano Geométrico aqui demonstrado serve de base para o famoso modelo Black & Scholes de precificação de opções, o qual assume que o ativo subjacente à opção (por exemplo, a ação de uma empresa) tem seu preço formado por um processo MBG.

Aug

2018

Conheça o modelo Fama French 3 Fatores

Apesar de o modelo de precificação de ativos CAPM de Sharpe-Lintner ser o mais conhecido no mundo das finanças e adminstração, este não é o melhor modelo para se explicar os retornos de ativos que carregam risco. Uma das opções mais difundidas, e que iniciou o movimento chamado modelo de fatores para precificação, conhecido no mercado também por modelos multi-fatores ou smart beta é o modelo de 3 fatores de Fama e French¹.

Neste modelo os retornos dos ativos é explicado não somente pelos retornos de mercado, o primeiro e principal fator, mas também por outros dois fatores conhecidos como SMB ( Small minus Big ) e HML ( High minus Low ), que referem-se respectivamente aos fatores de tamanho da firma e “valor” precificado, no qual a relação valor contábil sobre valor de mercado é a proxy. Uma ação com alta relação contábil sobre mercado é considerada uma empresa de “valor”, enquanto que no caso contrário se enquadram as chamadas empresas de “crescimento”, ou glamor.

As carteiras, que são construídas no final de junho de cada ano, são as interseções de duas carteiras formadas em tamanho ( Market Equity, ME ) e três carteiras formadas pela razão entre patrimônio líquido contábil e valor de mercado ( Book-to-Equity e Market Equity, BE/ME). O ponto de corte de tamanho para o ano t é o patrimônio mediano de mercado da Bolsa de Valore de Nova Iorque – NYSE, no final de junho do ano t. A métrica BE/ME para junho do ano t é o patrimônio contábil do último exercício encerrado em t-1 dividido por ME para dezembro de t-1. Os pontos de corte para BE/ME são os percentis 30% e 70% da NYSE. Desta forma são criados os seguintes seis portfólios:

	Firmas Pequenas	Firmas Grandes
Ações Valor	Small Value	Big Value
Ações Neutras	Small Neutral	Big Neutral
Ações Crescimento	Small Growth	Big Growth

Estes dois fatores extras são construídos a partir de seis carteiras do tipo long-short, determinadas pela interseção entre os dois critérios de classificação, tamanho e valor. Assim o fator SMB é calculado através da média dos retornos das empresas pequenas menos a média dos retornos das empresas grandes.

$SMB = 1/3 (Small Value + Small Neutral + Small Growth)\ \qquad \qquad – 1/3 (Big Value + Big Neutral + Big Growth)$

Da mesma forma, o fator HML é construído por uma carteira long-short montada com a média dos retornos das empresas de valor menos a média do retorno das empresas de crescimento.

$HML = 1/2 (Small Value + Big Value) – 1/2 (Small Growth + Big Growth)$

O fator de mercado é a carteira formada com todas as empresas listadas nas bolsas do país ponderadas pelo seu valor de mercado. O retorno do fator é, assim como no CAPM, o retorno em excesso ao ativo livre de risco. De posse dos retornos de nossos três fatores, o modelo de precificação de Fama e French segue a relação:

$$R_a = R_f + \beta (R_m – R_f) + \beta_s SMB + \beta_v HML$$

onde o retorno em excesso do ativo de interesse, $R_a – R_f$ é explicado pelo familiar $\beta$ de mercado, como no CAPM, mas também pelos recém introduzidos fatores SMB e HML, com exposições $\beta_s$ e $\beta_v$ respectivamente.

Por exemplo, se nosso ativo de interesse for uma ação de “valor” espera-se que a exposição ao fator HML seja alta, ou seja, $\beta_v$ será um valor relativamente elevado (quando em comparação com ações de crescimento). Com esta maior exposição ao fator valor, esta ação capturará melhor os retornos proporcionados por HML que não estão incluídos no mercado. Fama e French (1993)² argumentam que seu modelo explica muito melhor a seção cruzada (cross section) dos retornos das ações que o modelo mais simples, CAPM. Enquanto que este explica aproximadamente 60 a 70% dos retornos das ações, seu modelo multi-fatores é capaz de explicar mais de 90% das variações ocorridas nos preços.

Este modelo foi um dos precursores dos modelos multi-fatores que hoje estão em voga no mercado. Atualmente estes modelos estão inseridos dentro de “estilos de investimento”, onde por exemplo, uma determinada carteira pode ser formada com exposição unitária ao fator de mercado mais um viés para ações de valor. Diz-se que esta carteira está inserida no estilo “valor” de investimento. Com esta alocação o retorno esperado da carteira será o retorno esperado do mercado, pois seu beta de mercado é unitário, mais a exposição desta carteira ao fator valor vezes o retorno esperado deste fator. Se o fator valor possuir retorno esperado positivo esta carteira pode se beneficiar e bater o mercado.

Mas os fatores SMB e HML de fato possuem valor esperado de retorno positivos? O professor Kenneth French mantém em seu site pessoal um grande banco de dados com os históricos destes fatores e vários outros. É uma biblioteca bastante rica em dados que vários pesquisadores utilizam e pode ser acessada de forma livre em: http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/data_library.html. Abaixo apresentamos um gráfico de série temporal dos três fatores, mercado, tamanho e valor. Lembrando que os retornos dos fatores tamanho e valor já estão em excesso ao fator mercado, ou seja, uma carteira exposta a SMB é remunerada tanto pelo mercado quanto pelo fator em si.

A cada dia novos fatores vêm sendo descobertos e alguns desbancados, sempre na busca de um modelo ideal de precificação que una parcimônia na quantidade de fatores explicativos, boa aderência aos dados empíricos e mais recentemente, com fundamentação em teoria econômica para explicar sua validade. Considerando que estes fatores podem ser isolados do retorno de mercado e investidos de forma individualizada e cumulativa, não é coincidência que hoje vivemos uma explosão de produtos “multi-fatores”, “com estilo”, “smart beta” e afins.

Fama, E. F., & French, K. R. (1992). The cross‐section of expected stock returns. the Journal of Finance, 47(2), 427-465. ↩
Fama, E. F., & French, K. R. (1993). Common risk factors in the returns on stocks and bonds. Journal of financial economics, 33(1), 3-56. ↩

Rafael F. Bressan

Smile de Volatilidade parte 2

Estrutura a termo

Arbitragem estática

Arbitragem de borboleta

Arbitragem de calendário

Limites de inclinação

Distribuição implícita

Conclusão

Referências

Smile de Volatilidade

Reparametrizando B&S e definição de moneyness

Características de smiles de volatilidade

Mercados cambiais

Mercados de equities

Smile como forma de precificação

Conclusão

O Modelo Black-Scholes-Merton

Simulação de Monte Carlo

Simulação de Monte Carlo

Implementação em R

Processos Estocásticos para Finanças: uma introdução

Processos de Markov

Movimento Browniano

Definição

Movimento Browniano Geométrico

Conheça o modelo Fama French 3 Fatores

Blogpost

Archives