Mercado Futuro de Cupom Cambial (DDI e FRC)
Esse artigo tem por objetivo explorar o funcionamento do mercado futuro de cupom cambial, o qual pertence ao complexo de derivativos de juros e se mostra extremamente importante para montagem de hedges por parte de empresas que têm de lidar com a variação cambial em suas operações, bem como para investidores institucionais, como fundos de investimento, bancos, family offices, seguradoras e fundos de pensão, os quais buscam gerar retornos ao operar os instrumentos desse mercado.
O QUE É O CUPOM CAMBIAL?
O cupom cambial é a denominação dada à taxa de juros calculada pelo diferencial entre a taxa de juros interna e a variação cambial, ambos referentes a um mesmo período. Portanto, trata-se de uma taxa de juro em dólar. Em outras palavras, o cupom cambial representa a remuneração de um título expresso ou indexado em dólares no mercado financeiro nacional. De uma maneira mais simplificada, é o rendimento em dólares para estrangeiros que assumem o risco de investir no Brasil.
Vamos a um exemplo simples para um melhor entendimento:
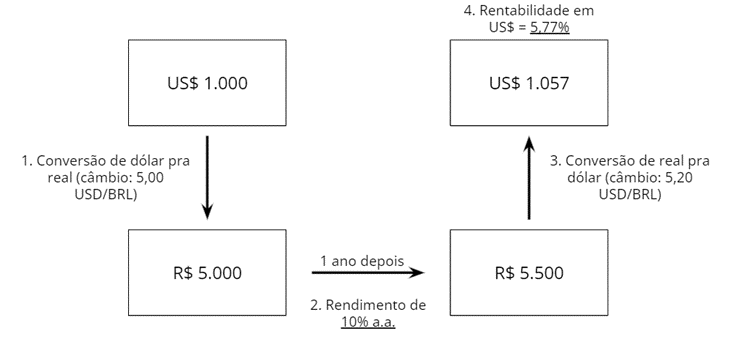
Assim sendo, fica claro que a rentabilidade dos recursos estrangeiros investidos no mercado nacional, quando da repatriação destes, pode divergir do retorno obtido na moeda local a depender da variação cambial do período. E esse verdadeiro rendimento dos recursos estrangeiros é representado pelo cupom cambial, o qual é calculado da seguinte maneira:

Sendo:
iaa = taxa de juros do investimento em moeda local expressa em percentual ao ano
du = período em dias úteis
ΔCambial = US$final/US$inicial
dc = período em dias corridos (variável necessária já que o cupom cambial é uma taxa de juros expressa em percentual ao ano e base 360 dias corridos)
Observe que a taxa do cupom é diretamente proporcional à taxa de juros interna, enquanto que a variação cambial atua de forma inversamente proporcional. Ou seja, aumentos na taxa de juros interna a qual o capital está exposto e uma valorização do real frente ao dólar no período resultam num maior cupom cambial.
Para o exemplo anterior, o cálculo do cupom cambial se daria da seguinte forma:

CUPOM CAMBIAL ENTRE HOJE E UMA DATA FUTURA
A partir das cotações dos contratos futuros de DI de 1 dia (código de negociação DI1) e de taxa de câmbio de Reais/Dólar dos Estados Unidos (código de negociação DOL), é possível obter a expectativa do mercado para o cupom cambial para diversos períodos futuros – diferentemente do que foi feito no exemplo anterior, no qual calculou-se o cupom cambial para um evento passado.
Para tanto, calcula-se o diferencial entre:
· a taxa de juros negociada pelo mercado para um determinado vértice da ETTJ (Estrutura a Termo da Taxa de Juros) através dos contratos futuros de DI
· e a variação cambial implícita no contrato futuro de dólar para o mesmo período em questão, ou seja, a quociente entre o Dólar Futuro e o Dólar Spot (também chamado de dólar “à vista” ou “pronto”).

Sendo:
iaa = taxa de juros negociada no DI1 do vértice equivalente ao período em questão, em percentual ao ano
du = período em dias úteis entre o dia da negociação, inclusive, e o último dia de negociação dos contratos futuros (ou seja, o último dia útil do mês anterior ao mês de vencimento), inclusive
dc = período em dias corridos entre o dia da negociação, inclusive, e o último dia de negociação dos contratos futuros (ou seja, o último dia útil do mês anterior ao mês de vencimento), inclusive
US$ Fut = cotação do câmbio negociada no contrato futuro de dólar para o período em questão
US$ Spot = taxa de câmbio do dia da negociação no mercado spot
PU do DI1 = preço unitário do contrato futuro de DI para o período em questão no dia da negociação (isso porque o valor final de liquidação do contrato (valor de face) do DI1 é de R$100.000,00 e, assim, seu PU (preço do contrato em uma determinada data) é obtido a partir do desconto do valor de face pela taxa negociada. Desse modo, ao dividir o valor de face pelo preço unitário do contrato no dia da negociação, encontra-se o mesmo resultado de (1 + iaa)du/252 ).
CONTRATO FUTURO DE CUPOM CAMBIAL (DDI)
Com isso em mente, podemos tratar do contrato futuro de cupom cambial (código de negociação DDI) propriamente dito.
Sua negociação teve início em 1998 na BM&F, quando veio substituir o uso combinado, pelos agentes do mercado, dos contratos futuros de dólar e de DI de 1 dia. Os principais agentes que negociam esse contrato são investidores institucionais, instituições financeiras e investidores estrangeiros.
Esse derivativo financeiro tem como objeto de negociação a taxa de juro obtida a partir do cálculo do diferencial entre:
· a expectativa de acumulação da taxa DI no período compreendido entre a data de operação, inclusive, e a data de vencimento do contrato futuro, exclusive (encontrada, como abordado anteriormente, por meio da taxa negociada no contrato futuro de DI de vencimento equivalente)
· e a expectativa de variação da taxa de câmbio (considerando a PTAX de venda como base) observada entre o dia útil anterior à data da operação, inclusive, e a data de vencimento do contrato, exclusive
Como pode ser notado, o cálculo do cupom cambial utilizado como objeto de negociação no DDI diverge – de modo sutil – daquele abordado anteriormente, uma vez que ele não toma como base o Dólar Spot para determinar da expectativa do mercado em relação a variação cambial para o período, mas, sim, a taxa PTAX (índice de taxa de câmbio calculado e divulgado diariamente pelo Bacen) do dia anterior, mais especificamente, a de venda.
Esse padrão foi adotado pelo fato de ser mais conveniente e menos complicado negociar uma taxa de juros em dólar (cupom cambial) com base numa taxa de câmbio que já está dada (PTAXD-1) em detrimento de uma que está constantemente sofrendo variações no momento da negociação (Dólar Spot).
Desse modo, existe uma clara defasagem ocasionada pela variação da taxa de câmbio entre o dia anterior e o dia da negociação do contrato e, por causa disso, convencionou-se no mercado financeiro brasileiro que, quando calculado pela PTAXD-1, denomina-se o cupom cambial como “cupom cambial sujo”. De forma oposta, chama-se de “cupom cambial limpo” aquele que é calculado com base no dólar à vista e, dessa maneira, não é contaminado pela volatilidade diária da taxa de câmbio, isto é, sem o efeito da defasagem de um dia presente no cupom sujo.
Ainda em relação a sua operacionalização, os contratos futuros de cupom cambial são negociados em taxa de juro, referente à cotação do cupom cambial para determinado período no momento da operação, a qual é expressa em percentual ao ano, linear, base 360 dias corridos, com até três casas decimais. Já o registro da operação é feito pelo seu Preço Unitário (PU), sendo este expresso com duas casas decimais. Em outras palavras, todas as operações de compra e venda de DDI são contratadas em taxa, mas são transformadas automaticamente em posições, em PU, de natureza contrária ao que foi transacionado durante o pregão, situação essa que será melhor abordada alguns parágrafos à frente, não se preocupe!
É importante entender, também, que, no vencimento do contratos futuros de cupom cambial, assim como ocorre com os contratos futuros de DI – como já abordado, de modo breve, no presente artigo –, seu PU vale, por regra, 100.000 pontos, ou seja, o valor final de liquidação do contrato (Valor de Face) é igual a cem mil pontos.
Contudo, diferentemente do que acontece com o DI1, cujos pontos valem, cada um, R$1,00 (resultando num valor de face de R$100.000,00), nos futuros de cupom cambial cada ponto do contrato é igual a US$0,50 e, assim, o PU no vencimento equivale a US$50.000,00.
Assim sendo, tão logo a montagem de posição em DDI é realizada, gera-se um PU da operação, o qual é, então, calculado ao trazer os 100.000 pontos do valor de face do contrato a valor presente utilizando como taxa de desconto a taxa do cupom ao ano negociada (i), conforme a seguinte fórmula:
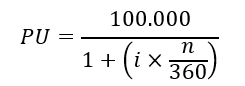
Sendo:
n = o número de dias corridos desde a data da negociação, inclusive, até o vencimento do contrato, exclusive
Fica claro, dessa maneira, a relação inversamente proporcional que é mantida entre a taxa do cupom cambial e o preço unitário do contrato futuro de cupom cambial e, portanto:
· a compra de taxa gera uma posição vendida em PU
· a venda de taxa gera uma posição comprada em PU
A razão dessa característica é facilmente compreendida quando a relação inversa das duas variáveis (taxa e PU) é atentamente analisada. Vamos lá:
· Caso se deseje, independentemente do motivo, ganhar com a alta da taxa de cupom cambial, compra-se taxa, ou seja, compra-se DDI. Contudo, como essa compra de taxa é registrada em PU, e essa variável é inversamente proporcional a i, gera-se uma posição vendida em PU, porque, desse modo, uma variação positiva na taxa (cenário considerado na montagem dessa posição hipotética) gerará uma diminuição no preço unitário do contrato, e uma posição vendida em PU condiz com essa realidade.
· De maneira oposta, caso se deseje ganhar com uma queda na taxa de cupom cambial, entra-se short em taxa, ou seja, monta-se uma posição vendida em taxa e, para tanto, vende-se DDI. Porém, como essa venda de taxa é registrada em PU, e essa variável é inversamente proporcional a i, gera-se uma posição long em PU, porque, desse modo, uma variação negativa na taxa (cenário considerado na montagem dessa posição hipotética) gerará uma valorização no preço unitário do contrato, e uma posição comprada em PU se beneficia desse acontecimento.
Depois das compras e vendas de DDI terem sido transformadas em posições short e long em PU, respectivamente, no final de cada pregão essas posições serão ajustadas com base no preço de ajuste do dia, determinado segundo regras estabelecidas pela B3, com movimentação financeira no dia da sessão de negociação subsequente. Esses ajustes diários são realizados automaticamente pelo sistema da B3, uma vez que ela se responsabiliza pela intermediação entre compradores e vendedores dos derivativos pertencentes ao mercado futuro, ou seja, a B3 atua como contraparte central e, portanto, age como uma proteção frente ao risco da contraparte não arcar com suas responsabilidades e obrigações (counterparty risk).
O valor do ajuste diário calculado pela B3:
· se positivo, será creditado ao comprador da posição em PU (vendedor original em taxa) e debitado ao vendedor da posição em PU (comprador original em taxa), ou seja, o agente comprado em PU (vendido em DDI) recebe o valor financeiro equivalente ao ajuste do agente vendido em PU (comprado em DDI);
· se negativo, o fluxo contrário acontecerá, ou seja, será debitado ao comprador da posição em PU o montante equivalente ao valor do ajuste diário e, então, creditado ao agente short em PU.
FRA DE CUPOM CAMBIAL (FRC)
Como já explorado, o DDI tem como objeto de negociação o cupom cambial dito “sujo”, pois utiliza em seus cálculos a taxa PTAXD-1 e, portanto, possui uma grande desvantagem em seu uso ao se mostrar exposto à variação cambial ocorrida entre o dia anterior e o data da negociação do contrato propriamente dita.
Assim sendo, em janeiro de 2001, a BM&F lançou uma modalidade operacional no mercado futuro de cupom cambial com o propósito de permitir e facilitar a realização de FRA (Forward Rate Agreement) de cupom cambial, cujo código de negociação é FRC, pelos agentes do mercado interessados.
FRA de cupom cambial (ou FRC) é uma operação sintética que utiliza dois contratos de DDI de vencimentos diferentes, e naturezas opostas, para retirar a variação cambial do dia anterior, e, desse modo, tal operação limpa o cupom sujo presente no DDI. A taxa resultante é uma taxa forward, livre da exposição à volatilidade diária da taxa de câmbio presente em um contrato de cupom cambial individual.
Esse contrato, além de possibilitar a negociação do diferencial de duas taxas futuras de cupom cambial e, portanto, gerar uma cupom cambial limpo, ou seja, mostrar-se como uma alternativa à defasagem da variação cambial de um dia existente no DDI, também se apresenta como um instrumento de muito mais liquidez no mercado quando comparado ao DDI, sendo, assim, bem mais presente no dia a dia dos bancos, gestoras, family offices etc.
Para efeito de negociação, as operações de FRC são realizadas como se fosse um novo contrato, ou seja, têm código de negociação próprio e se sujeita a todas as regras de pregão existentes para os demais contratos futuros. A diferença é a de que, em vez de gerar posições em um novo tipo de contrato, as operações de FRC são automaticamente transformadas pelo sistema da B3 em duas outras operações de DDI:
· a primeira, uma posição em DDI de mesma natureza e com vencimento idêntico ao negociado no FRC (ponta longa)
· e a segunda, uma posição em DDI de natureza inversa, para o primeiro vencimento de DDI existente (ponta curta)
A partir do penúltimo dia de negociação do primeiro vencimento de DDI, a segunda operação (ponta curta) será gerada no segundo vencimento de DDI, mantendo-se esse vencimento até o penúltimo dia de negociação desse novo contrato, quando o processo se repetirá. Ou seja, a Bolsa se encarrega de fazer essa rolagem da ponta curta automaticamente para o comprador/vendedor de FRC.
Em outras palavras, por meio desta operação, as partes assumem uma posição no vencimento do FRA (que corresponde a uma posição longa em DDI, com vencimento em t2) e, automaticamente, a Bolsa abre uma posição inversa no primeiro vencimento em aberto de DDI (com liquidação em t1).
O exemplo abaixo representa de modo ilustrativo uma situação hipotética em que se buscou montar uma posição comprada em FRC para t2.

Sendo assim, a operação de compra desse contrato foi realizada normalmente pelo agente de mercado, porém essa posição foi automaticamente convertida em uma posição long em DDI para vencimento em t2 (equivalente a ponta longa da operação) e uma posição short em DDI para o vencimento de data mais próxima ao momento da operação, nesse caso, t1 (equivalente a ponta curta da operação).
As partes, portanto, negociam uma taxa de juro anual linear, base 360, para um período futuro entre t1 e t2, ou seja, entre o dia da liquidação do DDI da ponta curta e o dia de liquidação do DDI de vencimento mais distante.
CONCLUSÃO
O mercado futuro de cupom cambial possui uma importância ímpar para o mercado financeiro brasileiro e os agentes que atuam nele. Esse artigo buscou, portanto, traçar uma linha de raciocínio de fácil entendimento para abordar e esclarecer, de modo introdutório, seus principais conceitos e os instrumentos financeiros que o compõe, bem como os detalhes acerca do funcionamento e da operacionalização destes derivativos.
Gostaria, por fim, de deixar registrado um agradecimento especial a Marilia Fontes, sócia-fundadora e analista de Renda Fixa na Nord Research, a qual se mostrou muito gentil e solícita em nossa breve conversa sobre o tema deste artigo, bem como sobre o material que foi produzido. A Marilia iniciou sua carreira na Mauá Capital sendo responsável pelas Mesas de Renda Fixa e de Câmbio e, assim, operou por muito tempo cupom cambial. Portanto, agradeço imensamente o feedback que me foi dado!
REFERÊNCIAS
MUNHOZ, Ygor. Os determinantes macroeconômicos da estrutura a termo das taxas de juros em dólar no brasil. Fundação Getúlio Vargas, São Paulo, 2015. Disponível em: <https://bibliotecadigital.fgv.br/dspace/bitstream/handle/10438/13994/Os%20determinantes%20macroecon%C3%B4micos%20da%20estrutura%20a%20termo%20das%20taxas%20de%20juros….pdf>. Acesso em: 20 de novembro de 2021.
BM&F. Mercado Futuro De Cupom Cambial. São Paulo, 2007. Disponível em: <https://silo.tips/download/instituto-educacional-bmf-mercado-futuro-de-cupom-cambial>. Acesso em: 20 de novembro de 2021.
FONTES, Marilia. O que é Cupom Cambial?. Youtube, Nord Research, 2020. Disponível em: <https://www.youtube.com/watch?v=WJY-mWRerQQ>. Acesso em: 20 de novembro de 2021.
GODOY, Carlos. Mercados e Instrumentos Financeiros II: Futuros de Câmbio – Cupom Cambial DDI. Universidade São Paulo, São Paulo. Disponível em: <https://edisci0plinas.usp.br/mod/resource/view.php?id=1210938>. Acesso em: 20 de novembro de 2021.
WANDERLEY, Peter. Estrutura a termo da taxa de juros e cupom cambial: decomposição em fatores principais. Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, 2018. Disponível em: <http://www.econ.puc-rio.br/uploads/adm/trabalhos/files/Peter_Kurthy_Wanderley_Mono_18_2.pdf>. Acesso em: 20 de novembro de 2021.
VIOLA, A. P., GUTIERREZ, M. S., LION, O. B., BARBEDO, C. H. Impacto dos swaps cambiais na curva de cupom cambial: uma análise segundo a regressão de componentes principais, 2009. Brazilian Business Review, Vol. 10. n. 1 (2013), 81-105. Disponível em: <https://www.bcb.gov.br/pec/wps/port/wps198.pdf>. Acesso em: 20 de novembro de 2021.
BM&F. Outras Operações Estruturadas: Operação de Forward Rate Agreement (FRA) de Cupom Cambial. Disponível em: <http://www.bmf.com.br/bmfbovespa/pages/boletim1/bd_manual/outras-Operacoes-estruturadas.asp>. Acesso em: 20 de novembro de 2021.
B3. Contrato Futuro de Taxa Média de Depósitos Interfinanceiros de Um Dia – DI1. Disponível em: <https://www.b3.com.br/pt_br/produtos-e-servicos/negociacao/juros/futuro-de-taxa-media-de-depositos-interfinanceiros-de-um-dia.htm>. Acesso em: 20 de novembro de 2021.
B3. Contrato Futuro de Taxa de Câmbio de Reais por Dólar Comercial – DOL. Disponível em: <https://www.b3.com.br/pt_br/produtos-e-servicos/negociacao/moedas/futuro-de-taxa-de-cambio-de-reais-por-dolar-comercial.htm>. Acesso em: 20 de novembro de 2021.
B3. Contrato Futuro de Cupom Cambial de Depósitos Interfinanceiros de Um Dia – DDI. Disponível em: <https://www.b3.com.br/pt_br/produtos-e-servicos/negociacao/juros/futuro-de-cupom-cambial-de-depositos-interfinanceiros-de-um-dia.htm>. Acesso em: 20 de novembro de 2021.
B3. Operações Estruturadas de Forward Rate Agreement de Cupom Cambial – FRC. Disponível em: <https://www.b3.com.br/pt_br/produtos-e-servicos/negociacao/juros/operacoes-estruturadas-de-forward-rate-agreement-de-cupom-cambial.htm>. Acesso em: 20 de novembro de 2021.